A post by Josh Givens, PhD student on the Compass programme.

Density ratio estimation is a highly useful field of mathematics with many applications. This post describes my research undertaken alongside my supervisors Song Liu and Henry Reeve which aims to make density ratio estimation robust to missing data. This work was recently published in proceedings for AISTATS 2023.

Density Ratio Estimation

Definition

As the name suggests, density ratio estimation is simply the task of estimating the ratio between two probability densities. More precisely for two RVs (Random Variables) $Z^0, Z^1$ on some space $\mathcal{Z}$ with probability density functions (PDFs) $p_0, p_1$ respectively, the density ratio is the function $r^*:\mathcal{Z}\rightarrow\mathbb{R}$ defined by

$r^*(z):=\frac{p_0(z)}{p_1(z)}$ .

Plot of the scaled density ratio alongside the PDFs for the two classes.

Density ratio estimation (DRE) is then the practice of using IID (independent and identically distributed) samples from $Z^0$ and $Z^1$ to estimate $r^*$ . What makes DRE so useful is that it gives us a way to characterise the difference between these 2 classes of data using just 1 quantity, $r^*$ .

The Density Ratio in Classification

We now give demonstrate this characterisability in the case of classification. To frame this as a classification problem define $Y\sim\text{Bernoulli}(0.5)$ and $Z$ by $Z|Y=y\sim Z^{y}$ . The task of predicting $Y$ given $Z$ using some function $\phi:\mathcal{Z}\rightarrow\{0,1\}$ is then our standard classification problem. In classification a common target is the Bayes Optimal Classifier, the classifier $\phi^*$ which maximises $\mathbb{P}(Y=\phi(Z)).$ We can write this classifier in terms of $r^*$ as we know that $\phi^*(z)=\mathbb{I}\{\mathbb{P}(Y=1|Z=z)>0.5\}$ where $\mathbb{I}$ is the indicator function. Then, by the total law of probability, we have

$\mathbb{P}(Y=1|Z=z)=\frac{p_{Z|Y=1}(z)\mathbb{P}(Y=1)}{p_{Z|Y=1}(z)\mathbb{P}(Y=1)+p_{Z|Y=0}(z)\mathbb{P}(Y=0)}$

$=\frac{p_1(z)\mathbb{P}(Y=1)}{p_1(z)\mathbb{P}(Y=1)+p_0(z)\mathbb{P}(Y=0)} =\frac{1}{1+\frac{1}{r}\frac{\mathbb{P}(Y=0)}{\mathbb{P}(Y=1)}}.$

Hence to learn the Bayes optimal classifier it is sufficient to learn the density ratio and a constant. This pattern extends well beyond Bayes optimal classification to many other areas such as error controlled classification, GANs, importance sampling, covariate shift, and others. Generally speaking, if you are in any situation where you need to characterise the difference between two classes of data, it’s likely that the density ratio will make an appearance.

Estimation Implementation – KLIEP

Now we have properly introduced and motivated DRE, we need to look at how we can go about performing it. We will focus on one popular method called KLIEP here but there are a many different methods out there (see Sugiyama et al 2012 for some additional examples.)

The intuition behind KLIEP is simple: as $r^* \cdot p_0=p_1$ , if $\hat r\cdot p_0$ is “close” to $p_1$ then $\hat r$ is a good estimate of $r^*$ . To measure this notion of closeness KLIEP uses the KL (Kullback-Liebler) divergence which measures the distance between 2 probability distributions. We can now formulate our ideal KLIEP objective as follows:

$\underset{r}{\text{min}}~ KL(p_1|p_0\cdot r)$

$\text{subject to:}~ \int_{\mathcal{Z}}r(z)p_0(z)\mathrm{d}z=1$

where $KL(p|p')$ represent the KL divergence from $p$ to $p'$ . The constraint ensures that the right hand side of our KL divergence is indeed a PDF. From the definition of the KL-divergence we can rewrite the solution to this as $\hat r:=\frac{\tilde r}{\mathbb{E}[r(X^0)]}$ where $\tilde r$ is the solution to the unconstrained optimisation

$\underset{r}{\text{min}}~\mathbb{E}[\log (r(Z^1))]-\log(\mathbb{E}[r(Z^0)]).$

As this is now just an unconstrained optimisation over expectations of known transformations of $Z^0, Z^1$ , we can approximate this using samples. Given samples $z^0_1,\dotsc,z^0_n$ from $Z_0$ and samples $z^1_1,\dotsc,z^1_n$ from $Z_1$ our estimate of the density ratio will be $\hat r:=\left(\frac{1}{n}\sum_{i=1}^nr(z_i^0)\right)^{-1}\tilde r$ where $\tilde r$ solves

$\underset{r}{\min}~ \frac{1}{n}\sum_{i=1}^n \log(r(z^1_i))-\log\left(\frac{1}{n}\sum_{i=1}^n r(z^0_i)\right).$

Despite KLIEP being commonly used, up until now it has not been made robust to missing not at random data. This is what our research aims to do.

Missing Data

Suppose that instead of observing samples from $Z$ , we observe samples from some corrupted version of $Z$ , $X$ . We assume that $\mathbb{P}(\{X=\varnothing\}\cup \{X=Z\})=1$ so that either $X$ is missing or $X$ takes the value of $Z$ . We also assume that whether $X$ is missing depends upon the value of $Z$ . Specifically we assume $\mathbb{P}(X=\varnothing|Z=z)=\varphi(z)$ with $\varphi(z)$ not constant and refer to $\varphi$ as the missingness function. This type of missingness is known as missing not at random (MNAR) and when dealt with improperly can lead to biased result. Some examples of MNAR data could be readings take from a medical instrument which is more likely to err when attempting to read extreme values or recording responses to a questionnaire where respondents may be more likely to not answer if the deem their response to be unfavourable. Note that while we do not see what the true response would be, we do at least get a response meaning that we know when an observation is missing.

Missing Data with DRE

We now go back to density ratio estimation in the case where instead of observing samples from $Z^0,Z^1$ we observe samples from their corrupted versions $X^0, X^1$ . We take their respective missingness functions to be $\varphi_0, \varphi_1$ and assume them to be known. Now let us look at what would happen if we implemented KLIEP with the data naively by simply filtering out the missing-values. In this case, the actual density ratio we would be estimating would be

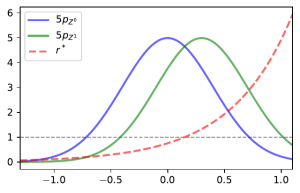
$r'(z):=\frac{p_{X_1|X_1\neq\varnothing}(z)}{p_{X_0|X_o\neq\varnothing}(z)}\propto\frac{(1-\varphi_1(z))p_1(z)}{(1-\varphi_0(z))p_0(z)}\not{\propto}r^*(z)$

and so we would get inaccurate estimates of the density ratio no matter how many samples are used to estimate it. The image below demonstrates this in the case were samples in class $1$ are more likely to be missing when larger and class $0$ has no missingness.

A plot of the density ratio using both the full data and only the observed part of the corrupted data

Our Solution

Our solution to this problem is to use importance weighting. Using relationships between the densities of $X$ and $Z$ we have that

$\mathbb{E}[g(Z)]=\mathbb{E}\left[\frac{\mathbb{I}\{X\neq\varnothing\}g(X)}{1-\varphi(X)}\right].$

As such we can re-write the KLIEP objective to keep our expectation estimation unbiased even when using these corrupted samples. This gives our modified objective which we call M-KLIEP as follows. Given samples $x^0_1,\dotsc,x^0_n$ from $X_0$ and samples $x^1_1,\dotsc,x^1_n$ from $X_1$ our estimate is $\hat r=\left(\frac{1}{n}\sum_{i=1}^n\frac{\mathbb{I}\{x_i^0\neq\varnothing\}r(x_i^0)}{1-\varphi_o(x_i^o)}\right)^{-1}\tilde r$ where $\tilde r$ solves

$\underset{r}{\min}~\frac{1}{n}\sum_{i=1}^n\frac{\mathbb{I}\{x_i^1\neq\varnothing\}\log(r(x_i^1))}{1-\varphi_1(x_i^1)}-\log\left(\frac{1}{n}\sum_{i=1}^n\frac{\mathbb{I}\{x_i^0\neq\varnothing\}r(x_i^0)}{1-\varphi_0(x_i^0)}\right).$

This objective will now target $r^*$ even when used on MNAR data.

Application to Classification

We now apply our density ratio estimation on MNAR data to estimate the Bayes optimal classifier. Below shows a plot of samples alongside the true Bayes optimal classifier and estimated classifiers from the samples via our method M-KLIEP and a naive method CC-KLIEP which simply ignores missing points. Missing data points are faded out.

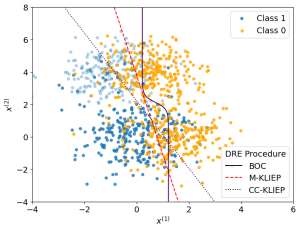
Faded points represent missing values. M-KLIEP represents our method, CC-KLIEP represents a Naive approach, BOC gives the Bayes optimal classifier

As we can see, due to not accounting for the MNAR nature of the data, CC-KLIEP underestimates the true number of class 1 samples in the top left region and therefore produces a worse classifier than our approach.

Additional Contributions

As well as this modified objective our paper provides the following additional contributions:

Theoretical finite sample bounds on the accuracy of our modified procedure.
Methods for learning the missingness functions $\varphi_1,\varphi_0$ .
Expansions to partial missingness via a Naive-Bayes framework.
Downstream implementation of our method within Neyman-Pearson classification.
Adaptations to Neyman-Pearson classification itself making it robust to MNAR data.

For more details see our paper and corresponding github repository. If you have any questions on this work feel free to contact me at josh.givens@bristol.ac.uk.

References

Givens, J., Liu, S., & Reeve, H. W. J. (2023). Density ratio estimation and neyman pearson classification with missing data. In F. Ruiz, J. Dy, & J.-W. van de Meent (Eds.), Proceedings of the 26th international conference on artificial intelligence and statistics (Vol. 206, pp. 8645–8681). PMLR.

Sugiyama, M., Suzuki, T., & Kanamori, T. (2012). Density Ratio Estimation in Machine Learning. Cambridge University Press.

A post by Jack Simons, PhD student on the Compass programme.

Introduction

I began my PhD with my supervisors, Dr Song Liu and Professor Mark Beaumont with the intention of combining their respective fields of research; Density Ratio Estimation (DRE), and Simulation Based Inference (SBI):

DRE is a rapidly growing paradigm in machine learning which (broadly) provides efficient methods of comparing densities without the need to compute each density individually. For a comprehensive yet accessible overview of DRE in Machine Learning see [1].
SBI is a group of methods which seek to solve Bayesian inference problems when the likelihood function is intractable. If you wish for a concise overview of the current work, as well as motivation then I recommend [2].

Last year we released a paper, Variational Likelihood-Free Gradient Descent [3] which combined these fields. This blog post seeks to condense, and make more accessible, the contents of the paper.

Motivation: Likelihood-Free Inference

Let’s begin by introducing likelihood-free inference. We wish to do inference on the posterior distribution of parameters $\theta$ for a specific observation $x=x_{\mathrm{obs}}$ , i.e. we wish to infer $p(\theta|x_{\mathrm{obs}})$ which can be decomposed via Bayes’ rule as

$p(\theta|x_{\mathrm{obs}}) = \frac{p(x_{\mathrm{obs}}|\theta)p(\theta)}{\int p(x_{\mathrm{obs}}|\theta)p(\theta) \mathrm{d}\theta}.$

The likelihood-free setting is that, additional to the usual intractability of the normalising constant in the denominator, the likelihood, $p(x|\theta)$ , is also intractable. In lieu of this, we require an implicit likelihood which describes the relation between data $x$ and parameters $\theta$ in the form of a forward model/simulator (hence simulation based inference!). (more…)

Tag: Density Ratio Estimation

Student Perspectives: Density Ratio Estimation with Missing Data