A post by Conor Newton, PhD student on the Compass programme.

Introduction

My research focuses on designing decentralised algorithms for the multi-agent variant of the Multi-Armed Bandit problem. This research is jointly supervised by Henry Reeve and Ayalvadi Ganesh.

(Image credit: Microsoft Research)

Many real-world optimisation problems involve repeated rather than one-off decisions. A decision maker (who we refer to as an agent) is required to repeatedly perform actions from a set of available options. After taking an action, the agent will receive a reward based on the action performed. The agent can then use this feedback to inform later decisions. Some examples of such problems are:

Choosing advertisements to display on a website each time a page is loaded to maximise click-through rate.
Calibrating the temperature to maximise the yield from a chemical reaction.
Distributing a budget between university departments to maximise research output.
Choosing the best route to commute to work.

In each case there is a fundamental trade-off between exploitation and exploration. On the one hand, the agent should act in ways which exploit the knowledge they have accumulated to promote their short term reward, whether that’s the yield of a chemical process or click-through rate on advertisements. On the other hand, the agent should explore new actions in order to increase their understanding of their environment in ways which may translate into future rewards.

Multi-Armed Bandits

The Multi-Armed Bandit problem is the prototypical example of a sequential decision making problem. The multi-armed bandit problem originates from a hypothetical scenario where a person is tasked with playing a series of slot-machines (colloquially known as a One-Arm Bandit), each having a payout unknown to player, with the aim of maximising profit.

Formally, the multi-armed bandit problem involves an environment consisting of a set of actions $\mathcal{A} = \{1, 2, \dots, K\}$ , commonly called arms, and corresponding unseen reward distributions $\{P_1, \dots, P_K\}$ . An agent follows an algorithm that will choose arms $I_t \in \mathcal{A}$ to play in every round $t = 1, \dots, T$ . After playing an arm $I_t \in \mathcal{A}$ , the agent receives a random reward $X_t \sim P_{I_t}$ , independent of past actions and rewards. The agent can use only the knowledge of the rewards received in previous rounds to choose subsequent actions.

Without loss of generality, we denote the expected values of the reward distributions by $\mu_1 > \mu_2 > \dots > \mu_K$ . Furthermore, we will assume that $P_1, \dots, P_K$ are Bernoulli distributions.

The performance of an algorithm is quantified by the regret. This measures how close the algorithm performs to a clairvoyant agent that always picks the best arm in each round. We define the regret after $T$ rounds as follows:

$\mathbb{E}[\mathcal{R}(T)] = T\mu_1 - \sum_{t=1}^T \mathbb{E}[X_t],$

In other words, the regret measures how much, on average, a perfectly rational agent would regret the decisions they’ve made, if they were informed about $\mu_1$ at the end of the game

The multi-armed bandit problem provides a framework which can be used to model the example problems introduced in the previous section.

The UCB Algorithm

The most influential frequentest algorithm in the multi-armed bandit literature is the UCB algorithm [1]. This algorithm has great theoretical guarantees and has seen a wide range of applications. It naturally balances the exploration vs exploitation trade-off, by selecting arms according to an upper-confidence bound derived from Hoeffding’s inequality. The upper-confidence bound of any arm $k$ at time $t$ is defined by,

$\mathrm{UCB} _k(t) := \underbrace{\hat\mu_k(t - 1)}_{\text{empirical mean}} + \underbrace{\sqrt{\frac{2 \log t}{T_k(t - 1)}}}_{\text{confidence term}},$

where $\hat\mu_k(t-1)$ is the empirical mean and $T_k(t - 1)$ is the number of plays of arm $k$ after round $t-1$ . In each round the arm with the highest UCB is selected and played.

$I_t = \text{argmax}_{k \in \{1, \dots, K\}} \mathrm{UCB}_k(t).$

The selected arm will either have a high empirical mean (exploitation) or a large confidence interval due to not being played a lot (exploration), this balances the exploration vs exploitation trade-off.

The UCB algorithm is proven to have the following upper-bound on its regret, which is tight up to constant factors,

$\mathbb{E}[\mathcal{R}(T)] \le \sum_{k = 2}^K \frac{16\log T}{\Delta_k} +3 \sum_{k = 1}^K \Delta_k,$

where $\Delta_k := \mu_1 - \mu_k$ . The two key features of this regret bound is the logarithmic scaling on $T$ and the dependence on the suboptimality gaps $\frac{1}{\Delta_k}$ . The following simulation results shows the effect of changing the suboptimality gap $\Delta_2$ on the regret, for an agent following the UCB algorithm.

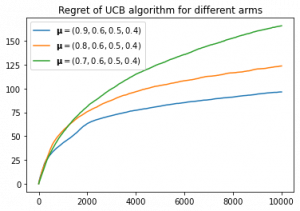
From these results, it can observed that smaller $\Delta_2$ corresponds to increased regret, this is because the agent has a harder time distinguishing the better arms. Additionally, the logarithmic scaling on $T$ is apparent.

There are many other algorithms for the multi-armed bandit problem which have similar theoretical results. A great reference is Bandit Algorithms [6].

Multi-Agent Multi-Armed Bandits

A natural extension to the multi-armed bandit problem is to consider multiple decision makers working on the same problem in parallel. This is motivated by the advent of distributed computing but more generally provides a framework for sequential decision making with multiple decision makers. A motivating example is a network of web servers tasked with dynamically selecting advertisements to be displayed each time a page is requested. Popular websites will often require multiple web servers to handle many users in parallel and in different geographical locations. The web servers should share information to accelerate learning which advertisements are the best to show.

Formally, this setting extends the single-agent multi-armed bandit problem to include $N$ agents, denoted $\{1, \dots, N\}$ , connected via network. The agents each play the multi-armed bandit problem in parallel over a time horizon $T$ . Between rounds, the agents can share information with their neighbours. To make this realistic, constraints on the number of bits communicated should be enforced. An agent can make decisions based on the rewards it has received and the information received from its neighbours.

The goal in the multi-agent section is to try to achieve similar total regret to that of a single agent preforming all $NT$ actions itself. A group of multiple agents with limited communication cannot hope to perform as well as a single agent, since each agent will be making decisions with only a subset of all the available information. Despite this, there are multiple multi-agent multi-armed bandits algorithms that achieve similar regret scaling to a single agent algorithm. One such example is the Gossip-Insert-Eliminate algorithm.

The Gossip-Insert-Eliminate Algorithm

The Gossip-Insert-Eliminate Algorithm [2] approaches the multi-agent multi-armed bandit problem by distributing the exploration process amongst the agents by partitioning the sets of arms between the agents. Each agent will play the UCB algorithm on this subset of arms. In addition to this, a mechanism is put in place to allow the good arms to be shared between the agents through a gossiping communication protocol. After a series of rounds, the agents will recommend their most played arm to a randomly chosen neighbour. The neighbour can then start playing this arm from the subsequent round. At any time, an agent may hold up to two arms received from recommendations, on receiving another recommendation it will discard the least played of the two.

The total regret of the Gossip-Insert-Eliminate algorithm has the following upper-bound if the agents are connected via the complete graph:

$\mathbb{E}[\mathcal{R}(T)] \le \sum_{k = 2}^K \frac{16\log T}{\Delta_k} + \underbrace{\mathcal{O}\left(\frac{K}{\Delta_2^4} + (\log N)^2\right)}_{\text{Regret from delay in receiving the best arm}}$

Similar to the single-agent UCB algorithm, the scaling of the regret bound depends of both $\log T$ and the suboptimality gap $\Delta_k$ . In addition to this, there is a second term that corresponds to the time it takes for all of the agents to receive the best arm. This term blows up as $\Delta_k$ decreases, since the best arm is harder to identify. The $\log N$ term corresponds to the time it takes for a rumour to spread on a complete graph.

The following results compare the performance of the Gossip-Insert-Eliminate algorithm to a single agent performing all $NT$ actions.

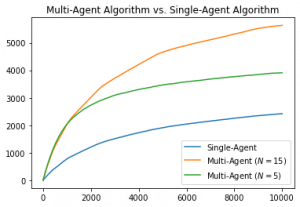
It can be seen in these results that there is an initial bump in regret where the agents are waiting to receive the best arm. This corresponds the second term in the regret bound.

In a recent paper [4], we have extended the gossip-insert-eliminate algorithm and have shown that it can attain the asymptotically optimal rate for a single agent. An alternative approach is to the multi-agent setting is to communicate reward estimates and aggregate this knowledge using a mean consensus algorithm. This approach is explored in [3].

Multi-armed Bandits in Metric Spaces

Whilst the classical formulation of the multi-armed bandit problem has a finite action set, there are many applications which can be more effectively modelled by an infinite action
space. For example, when optimising a chemical reaction, there is a continuum of potential temperatures and concentrations of inputs. Of course, over a finite time horizon, a learner can only try a finite number of actions. Hence, in order for this problem to be tractable, we must assume some additional structure on the relationship between the actions.

A convenient structure is to assume that the arms form a metric space $(\mathcal{A}, d)$ with respect a metric $d : \mathcal{A} \times \mathcal{A} \to \mathbb{R}$ . It can then be assumed that the arms that are close together in the metric space exhibit similar expected rewards. This assumption can be formalised through a Lipchitz-continuity condition on the expected reward of each arm:

$|\mu_x - \mu_y|< \mathrm{L} \cdot d(x, y)$

for any $x, y \in \mathcal{A}$ . This setting is referred to as the metric space multi-armed bandit problem.

The are numerous effective algorithms for the metric space multi-armed bandit problem. Many of which use the UCB algorithm and a discretetisation of the metric space which is iteratively refined. One such algorithm is the Zooming algorithm due to Kleinberg et al. [4]. On the unit interval with euclidean norm $([0, 1], |\cdot|)$ , the zooming algorithm achieves an optimal regret bound of order:

$\mathbb{E}[\mathcal{R}(T)] \le \tilde{\mathcal{O}}( T^{2/3}).$

The current iteration of my research will aim develop a multi-agent algorithm for the metric space multi-armed bandit problem.

Future Work

Beyond the problems introduced in this post, there are a number of open problems waiting to be solved in the multi-agent multi-armed bandit framework. Some examples include, the non-stationary setting where distributions of the rewards change over time or the existence malicious agents within the network who communicate adversarially with the intention of increasing the regret of other agents.

References

[1] Auer, P., Cesa-Bianchi, N., & Fischer, P. (2002). Finite-time analysis of the multiarmed bandit problem. Machine learning, 47(2), 235-256.

[2] Chawla, R., Sankararaman, A., Ganesh, A., & Shakkottai, S. (2020, June). The gossiping insert-eliminate algorithm for multi-agent bandits. In International Conference on Artificial Intelligence and Statistics (pp. 3471-3481). PMLR.

[3] Martínez-Rubio, D., Kanade, V., & Rebeschini, P. (2019). Decentralized cooperative stochastic bandits. Advances in Neural Information Processing Systems, 32.

[4] Newton, C., Ganesh, A., & Reeve, H. (2022). Asymptotic Optimality for Decentralised Bandits. ACM SIGMETRICS Performance Evaluation Review, 49(2), 51-53.

[5] Kleinberg, R., Slivkins, A., & Upfal, E. (2008, May). Multi-armed bandits in metric spaces. In Proceedings of the fortieth annual ACM symposium on Theory of computing (pp. 681-690).

[6] Lattimore, T., & Szepesvári, C. (2020). Bandit algorithms. Cambridge University Press.