A post by Dan Ward, PhD student on the Compass programme.
Normalising flows are black-box approximators of continuous probability distributions, that can facilitate both efficient density evaluation and sampling. They function by learning a bijective transformation that maps between a complex target distribution and a simple distribution with matching dimension, such as a standard multivariate Gaussian distribution.
Transforming distributions
Before introducing normalising flows, it is useful to introduce the idea of transforming distributions more generally. Lets say we have two uniform random variables, , and
. In this case, it is straight forward to define the bijective transformation
that maps between these two distributions, as shown below.
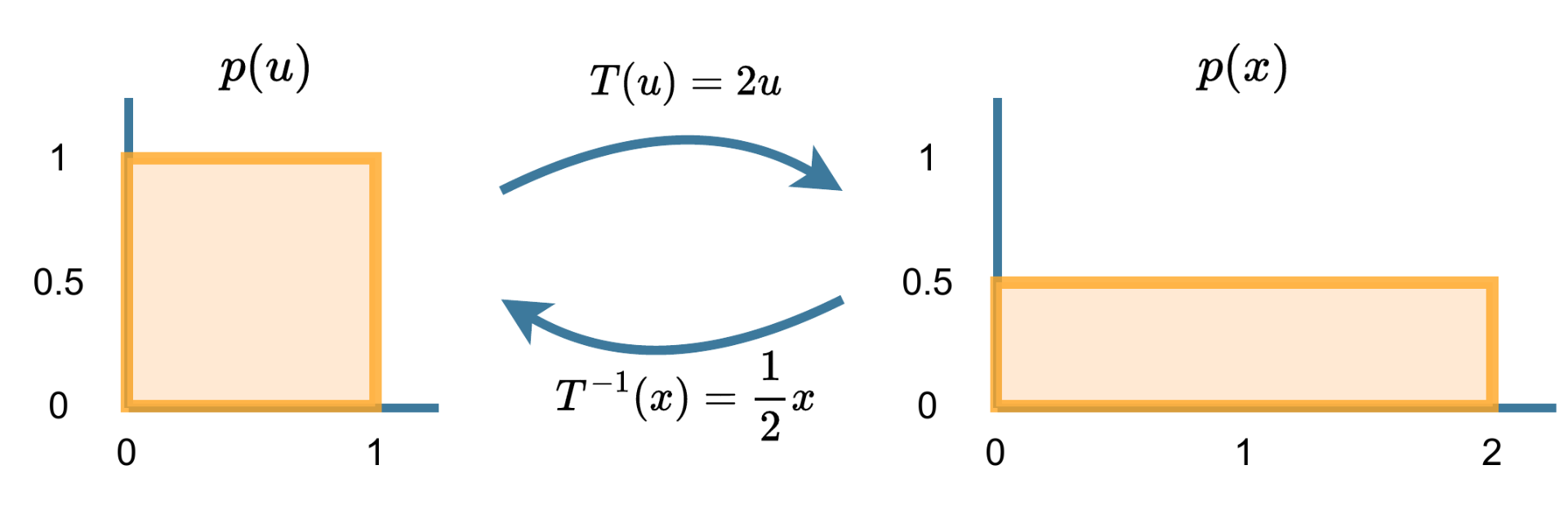
If we wished to sample , but could not do so directly, we could instead sample
, and then apply the transformation
. If we wished to evaluate the density of
, but could not do so directly, we can rewrite
in terms of
where is the density of the corresponding point in the
space, and dividing by 2 accounts for the fact that the transformation
stretches the space by a factor of 2, “diluting” the probability mass. The key thing to notice here, is that we can describe the sampling and density evaluation operations of one distribution,
, based on a bijective transformation of another, potentially easier to work with distribution,
.
This idea can be made more precise and be generalised to the multivariate case, using the change of variables formula
where is the Jacobian matrix for the transformation
, containing the partial derivatives
The absolute value of the Jacobian determinant, , measures the stretch induced by
. Intuitively, it is the ratio of the volume in an infinitesimally small region around
, to the corresponding infinitesimally small region in
. From equation 1, we can see that for a given
/
pair, if
, then
, as
expands the space in that region, diluting the probability mass. Conversely, if
, then
compresses the region, meaning
. Equivalently, we can also use the Jacobian of
to calculate
Normalising flows
Normalising flows are a simple extension of the above, in which we approximate a target distribution by learning a bijective transformation
, with parameters
, which maps from a tractable base density
to the approximation
. Once a flow model is trained, we can sample from the model
, by first sampling
, and then applying the transformation
. The density
can be calculated using equation 2.
Note that it is also straight forward to learn conditional distributions, by making the bijection depend on the conditioning variables (with no further constraints). However, for simplicity, we consider unconditional density estimation.
Choice of transformation
Much of recent normalising flow research has focused on the choice of . Specifically, there are three main properties to consider when choosing
- Flexibility. The transformation should be flexible enough to be able to mould the base distribution into the target density. One simple way to increase flexibility is to compose multiple bijections, i.e.
.
- Fast
and
computation. For density evaluation to be fast, both
and
must be fast to compute. Generally,
is constrained to be triangular, in which case the determinant can be efficiently computed as the product of the diagonal entries.
- Fast
. If fast sampling from the flow model is desired, then
must be fast to compute, so that we can efficiently transform samples from the base distribution to the target distribution.
In practice, there is often a trade off between these components that should be considered for the task at hand. There are a diverse range of choices for . Although the details of architectures will not be discussed here, a common approach is to use neural networks to parameterise easy to invert functions such as affine transformations or splines. More detail on the various approaches and their trade-offs can be found in Papamakarios et al. [2021].
For training we need some “information” about the target density, typically either samples from the target distribution, or the ability to evaluate the target density (potentially up to a normalising constant). We consider how to train a flow in these contexts in the next section.
Training
Using Samples. Training a flow using samples from a target density is straight forward, and can be achieved by minimising the negative log likelihood (maximum likelihood) with respect to the bijection parameters
where in the second line we substitute in equation 2. Note that this can equivalently be framed as minimising the “forward” Kullback-Leibler (KL) divergence between the true and approximate distributions as
The ability to fit flows by maximum likelihood is generally seen as a key advantage of normalising flows, making them simpler to train than other generative models such as generative adversarial networks.
Using density evaluations. In many areas of statistics, we can often only evaluate the density of a target distribution up to a normalising constant , i.e.
, where
is the true density, and we have access to
. In this case, we can minimise the “reverse” KL divergence to fit the flow model
where we make use of samples from the base distribution to approximate the expectation. This training procedure is commonly used in variational inference to approximate posterior distributions.
Flows in practice – flowjax
There are now many available packages that make it straight forward to use normalising flows. Here, I will show how normalising flows can be used in Python, using the flowjax Python package. It’s a great package with very easy to use Jax-based implementations of flows (disclaimer: I may be biased as the author of this package – other normalising flow packages are available, such as the PyTorch-based nflows).
First we need to import the required packages
from flowjax.distributions import Normal
from flowjax.flows import BlockNeuralAutoregressiveFlow
from flowjax.train_utils import train_flow
from jax import random
import jax.numpy as jnp
import import numpy as np
We can create some toy data, which are points following a chequered pattern
def get_chequered_data(n=100000):
x1 = np.random.rand(n) * 4 - 2
x2 = np.random.rand(n) - np.random.randint(0, 2, n) * 2
x2 = x2 + (np.floor(x1) % 2)
return jnp.column_stack((x1, x2))*2
x = get_chequered_data()
We can now create and train the flow. Here we use a block neural autoregressive flow model, as introduced by De Cao et al. [2020].
flowkey, trainkey = random.split(random.PRNGKey(1)) # Jax random seeds
base_dist = Normal(x.shape[1])
flow = BlockNeuralAutoregressiveFlow(flowkey, base_dist, block_size=(50, 50), nn_layers=3)
flow, _ = train_flow(trainkey, flow, x, learning_rate=1e-2, max_epochs=150, max_patience=20)
After training, we can evaluate the density of arbitrary points flow.log_prob(x[:10]), or sample (if is implemented)
flow.sample(key, n=10).Visualising the learned density, we can see the flow reasonably approximates the target density
The learned density
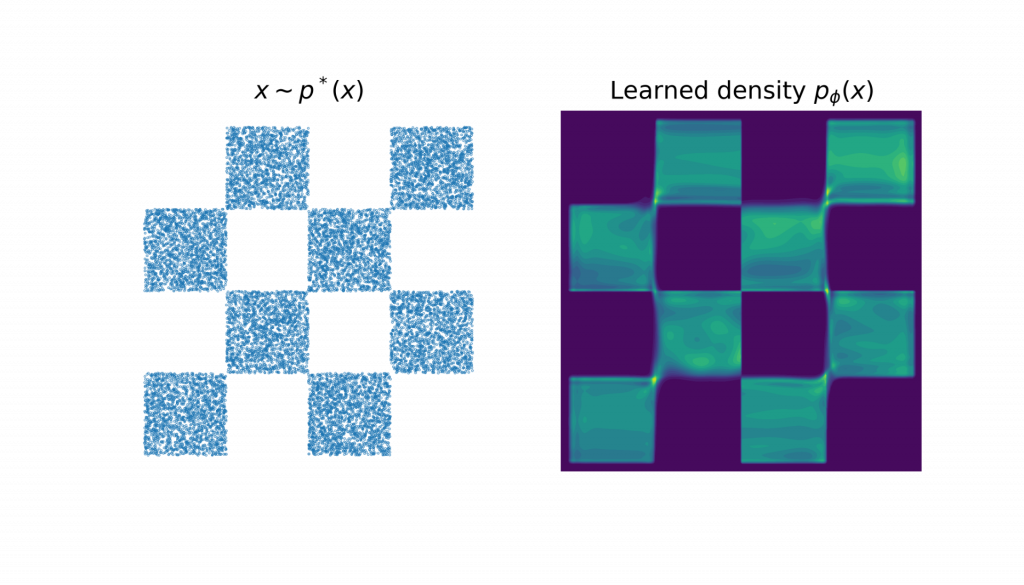
We can also visualise the learned transformation. Note the colours below are to give an indication of which points map to which between the two distributions.
The learned transformation

If you are interested in learning more about normalising flows, I would recommend this review paper by Papamakarios et al. [2020], for a more complete, but still introductory overview.
References
De Cao, N., Aziz, W. and Titov, I., 2020, August. Block neural autoregressive flow. In Uncertainty in artificial intelligence (pp. 1263-1273). PMLR.
Papamakarios, G., Nalisnick, E.T., Rezende, D.J., Mohamed, S. and Lakshminarayanan, B., 2021. Normalizing Flows for Probabilistic Modeling and Inference. J. Mach. Learn. Res., 22(57), pp.1-64.

