A post by Michael Whitehouse, PhD student on the Compass programme.
Introduction
September saw the first of an exciting new series of Compass industry focus labs; with this came the chance to make use of the extensive skill sets acquired throughout the course and an opportunity to provide solutions to pressing issues of modern industry. The partner for the first focus lab, Wessex Water, posed the following question: given time series data on water flow levels in pipes, can we detect if new leaks have occurred? Given the inherent value of clean water available at the point of use and the detriments of leaking this vital resource, the challenge of ensuring an efficient system of delivery is of great importance. Hence, finding an answer to this question has the potential to provide huge economic, political, and environmental benefits for a large base of service users.
Data and Modelling:
The dataset provided by Wessex Water consisted of water flow data spanning across around 760 pipes. After this data was cleaned and processed some useful series, such as minimum nightly and average daily flow (MNF and ADF resp.), were extracted. Preliminary analysis carried out by our collaborators at Wessex Water concluded that certain types of changes in the structure of water flow data provide good indications that a leak has occurred. From this one can postulate that detecting a leak amounts to detecting these structural changes in this data. Using this principle, we began to build a framework to build solutions: detect the change; detect a new leak. Change point detection is a well-researched discipline that provides us with efficient methods for detecting statistically significant changes in the distribution of a time series and hence a toolbox with which to tackle the problem. Indeed, we at Compass have our very own active member of the change point detection research community in the shape of Dom Owens. The preliminary analysis gave that there are three types of structural change in water flow series that indicate a leak: a change in the mean of the MNF, a change in trend of the MNF, and a change in the variance of the difference between the MNF and ADF. In order to detect these changes with an algorithm we would need to transform the given series so that the original change in distribution corresponded to a change in the mean of the transformed series. These transforms included calculating generalised additive model (GAM) residuals and analysing their distribution. An example of such a GAM is given by:
![\mathbb{E}[\text{flow}_t] = \beta_0 \sum_{i=1}^m f_i(x_i).](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5B%5Ctext%7Bflow%7D_t%5D+%3D+%5Cbeta_0+%5Csum_%7Bi%3D1%7D%5Em+f_i%28x_i%29.&bg=ffffff&fg=000000&s=0 "\mathbb{E}[\text{flow}_t] = \beta_0 \sum_{i=1}^m f_i(x_i).")
Where the x i ’s are features we want to use to predict the flow, such as the time of day or current season. The principle behind this analysis is that any change in the residual distribution corresponds to a violation of the assumption that residuals are independently, identically distributed and hence, in turn, corresponds to a deviation from the original structure we fit our GAM to.
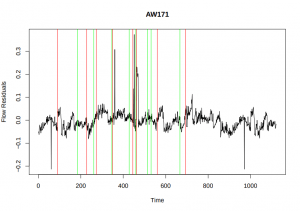
Figure 1: GAM residual plot. Red lines correspond to detected changes in distribution, green lines indicate a repair took place.
A Change Point Detection Algorithm:
In order to detect changes in real time we would need an online change point detection algorithm, after evaluating the existing literature we elected to follow the mean change detection procedure described in [Wang and Samworth, 2016]. The user-end procedure is as follows:
- Calculate mean estimate
on some data we assume is stationary.
- Feed a new observation into the algorithm. Calculate test statistics based on new data.
- Repeat (2) until any test statistics exceed a threshold at which point we conclude a mean change has been detected. Return to (1).
Due to our 2 week time restraint we chose to restrict ourselves to finding change points corresponding to a mean change, just one of the 3 changes we know are indicative of a leak. As per the fundamental principles of decision theory, we would like to tune and evaluate our algorithm by minimising some loss function which depends on some ‘training’ data. That is, we would like to look at some past period of time and make predictions of when leaks happened given the flow data across the same period, then we evaluate how accurate these predictions were and adjust or asses the model accordingly. However, to do this we would need to know when and where leaks actually occurred across the time period of the data, something we did not have access to. Without ‘labels’ indicating that a leak has occurred, any predictions from the model were essentially meaningless, so we sought to find a proxy. The one potentially useful dataset we did have access to was that of leak repairs. It is clear that a leak must have occurred if a repair has occurred, but for various reasons this proxy does not provide an exhaustive account of all leaks. Furthermore, we do not know which repairs correspond to leaks identified by the particular distributional change in flow data we considered. This, in turn, means that all measures of model performance must come with the caveat that they are contingent on incomplete data. If when conducting research we find out results are limited it is our duty as statisticians to report when this is the case – it is not our job to sugar coat or manipulate our findings, but to report them with the limitations and uncertainty that inextricably come alongside. Results without uncertainty are as meaningless as no results at all. This being said, all indications pointed towards the method being effective in detecting water flow data mean change points which correspond to leak repairs, giving a positive result to feedback to our friends at Wessex Water.
Final Conclusions:
Communicating statistical concepts and results to an audience of varied areas and levels of expertise is important now more than ever. The continually strengthening relationships between Compass and its industrial partners are providing students with the opportunity to gain experience in doing exactly this. The focus lab concluded with a presentation on our findings to the Wessex Water operations team, during which we reported the procedures and results. The technical results were well supported by the demonstration of an R shiny dashboard app, which provided an intuitive interface to view the output of the developed algorithm. Of course, there is more work to be done. Expanding the algorithm to account for all 3 types of distributional change is the obvious next step. Furthermore, fitting a GAM to data for 760 pipes is not very efficient. Additional investigations into finding ways to ‘cluster’ groups of pipes together according to some notion of similarity is a natural avenue for future work in order to reduce the number of GAMS we need to fit.This experience enabled students to apply skills in statistical modelling, algorithm development, and software development to a salient problem faced by an industry partner and marked a successful start to the Compass industry focus lab series.