A post by Harry Tata, PhD student on the Compass programme.
Oligonucleotides in Medicine
Oligonucleotide therapies are at the forefront of modern pharmaceutical research and development, with recent years seeing major advances in treatments for a variety of conditions. Oligonucleotide drugs for Duchenne muscular dystrophy (FDA approved) [1], Huntington’s disease (Phase 3 clinical trials) [2], and Alzheimer’s disease [3] and amyotrophic lateral sclerosis (early-phase clinical trials) [4] show their potential for tackling debilitating and otherwise hard-to-treat conditions. With continuing development of synthetic oligonucleotides, analytical techniques such as mass spectrometry must be tailored to these molecules and keep pace with the field.
Working in conjunction with AstraZeneca, this project aims to advance methods for impurity detection and quantification in synthetic oligonucleotide mass spectra. In this blog post we apply a regularised version of the Richardson-Lucy algorithm, an established technique for image deconvolution, to oligonucleotide mass spectrometry data. This allows us to attribute signals in the data to specific molecular fragments, and therefore to detect impurities in oligonucleotide synthesis.
Oligonucleotide Fragmentation
If we have attempted to synthesise an oligonucleotide  with a particular sequence, we can take a sample from this synthesis and analyse it via mass spectrometry. In this process, molecules in the sample are first fragmented — broken apart into ions — and these charged fragments are then passed through an electromagnetic field. The trajectory of each fragment through this field depends on its mass/charge ratio (m/z), so measuring these trajectories (e.g. by measuring time of flight before hitting some detector) allows us to calculate the m/z of fragments in the sample. This gives us a discrete mass spectrum: counts of detected fragments (intensity) across a range of m/z bins [5].
with a particular sequence, we can take a sample from this synthesis and analyse it via mass spectrometry. In this process, molecules in the sample are first fragmented — broken apart into ions — and these charged fragments are then passed through an electromagnetic field. The trajectory of each fragment through this field depends on its mass/charge ratio (m/z), so measuring these trajectories (e.g. by measuring time of flight before hitting some detector) allows us to calculate the m/z of fragments in the sample. This gives us a discrete mass spectrum: counts of detected fragments (intensity) across a range of m/z bins [5].
To get an idea of how much of  is in a sample, and what impurities might be present, we first need to consider what fragments
is in a sample, and what impurities might be present, we first need to consider what fragments  will produce. Oligonucleotides are short strands of DNA or RNA; polymers with a backbone of sugars (such as ribose in RNA) connected by linkers (e.g. a phosphodiester bond), where each sugar has an attached base which encodes genetic information [6].
will produce. Oligonucleotides are short strands of DNA or RNA; polymers with a backbone of sugars (such as ribose in RNA) connected by linkers (e.g. a phosphodiester bond), where each sugar has an attached base which encodes genetic information [6].
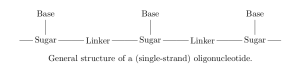
On each monomer, there are two sites where fragmentation is likely to occur: at the linker (backbone cleavage) or between the base and sugar (base loss). Specifically, depending on which bond within the linker is broken, there are four modes of backbone cleavage [7,8].
We include in  every product of a single fragmentation of
every product of a single fragmentation of 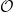 — any of the four backbone cleavage modes or base loss anywhere along the nucleotide — as well as the results of every combination of two fragmentations (different cleavage modes at the same linker are mutually exclusive).
— any of the four backbone cleavage modes or base loss anywhere along the nucleotide — as well as the results of every combination of two fragmentations (different cleavage modes at the same linker are mutually exclusive).

Sparse Richardson-Lucy Algorithm
Suppose we have a chemical sample which we have fragmented and analysed by mass spectrometry. This gives us a spectrum across n bins (each bin corresponding to a small m/z range), and we represent this spectrum with the column vector  , where
, where 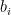 is the intensity in the
is the intensity in the 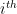 bin. For a set
bin. For a set  of possible fragments, let
of possible fragments, let 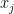 be the amount of
be the amount of 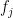 that is actually present. We would like to estimate the amounts of each fragment based on the spectrum
that is actually present. We would like to estimate the amounts of each fragment based on the spectrum 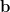 .
.
If we had a sample comprising a unit amount of a single fragment 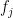 , so
, so 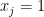 and
and 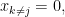 and this produced a spectrum
and this produced a spectrum  , we can say the intensity contributed to bin
, we can say the intensity contributed to bin 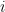 by
by 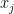 is
is  In mass spectrometry, the intensity in a single bin due to a single fragment is linear in the amount of that fragment, and the intensities in a single bin due to different fragments are additive, so in some general spectrum we have
In mass spectrometry, the intensity in a single bin due to a single fragment is linear in the amount of that fragment, and the intensities in a single bin due to different fragments are additive, so in some general spectrum we have 
By constructing a library matrix 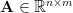 such that
such that  (so the columns of
(so the columns of 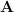 correspond to fragments in
correspond to fragments in  ), then in ideal conditions the vector of fragment amounts
), then in ideal conditions the vector of fragment amounts 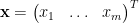 solves
solves 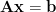 . In practice this exact solution is not found — due to experimental noise and potentially because there are contaminant fragments in the sample not included in
. In practice this exact solution is not found — due to experimental noise and potentially because there are contaminant fragments in the sample not included in  — and we instead make an estimate
— and we instead make an estimate  for which
for which 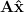 is close to
is close to 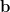 .
.
Note that the columns of 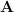 correspond to fragments in
correspond to fragments in  : the values in a single column represent intensities in each bin due to a single fragment only. We
: the values in a single column represent intensities in each bin due to a single fragment only. We 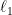 -normalise these columns, meaning the total intensity (over all bins) of each fragment in the library matrix is uniform, and so the values in
-normalise these columns, meaning the total intensity (over all bins) of each fragment in the library matrix is uniform, and so the values in  can be directly interpreted as relative abundances of each fragment.
can be directly interpreted as relative abundances of each fragment.
The observed intensities — as counts of fragments incident on each bin — are realisations of latent Poisson random variables. Assuming these variables are i.i.d., it can be shown that the estimate of 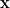 which maximises the likelihood of the system is approximated by the iterative formula
which maximises the likelihood of the system is approximated by the iterative formula

Here, quotients and the operator  represent (respectively) elementwise division and multiplication of two vectors. This is known as the Richardson-Lucy algorithm [9].
represent (respectively) elementwise division and multiplication of two vectors. This is known as the Richardson-Lucy algorithm [9].
In practice, when we enumerate oligonucleotide fragments to include in  , most of these fragments will not actually be produced when the oligonucleotide passes through a mass spectrometer; there is a large space of possible fragments and (beyond knowing what the general fragmentation sites are) no well-established theory allowing us to predict, for a new oligonucleotide, which fragments will be abundant or negligible. This means we seek a sparse estimate, where most fragment abundances are zero.
, most of these fragments will not actually be produced when the oligonucleotide passes through a mass spectrometer; there is a large space of possible fragments and (beyond knowing what the general fragmentation sites are) no well-established theory allowing us to predict, for a new oligonucleotide, which fragments will be abundant or negligible. This means we seek a sparse estimate, where most fragment abundances are zero.
The Richardson-Lucy algorithm, as a maximum likelihood estimate for Poisson variables, is analagous to ordinary least squares regression for Gaussian variables. Likewise lasso regression — a regularised least squares regression which favours sparse estimates, interpretable as a maximum a posteriori estimate with Laplace priors — has an analogue in the sparse Richardson-Lucy algorithm:
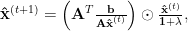
where 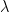 is a regularisation parameter [10].
is a regularisation parameter [10].
Library Generation
For each oligonucleotide fragment  , we smooth and bin the m/z values of the most abundant isotopes of
, we smooth and bin the m/z values of the most abundant isotopes of  , and store these values in the columns of
, and store these values in the columns of 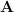 . However, if these are the only fragments in
. However, if these are the only fragments in  then impurities will not be identified: the sparse Richardson-Lucy algorithm will try to fit oligonucleotide fragments to every peak in the spectrum, even ones that correspond to fragments not from the target oligonucleotide. Therefore we also include ‘dummy’ fragments corresponding to single peaks in the spectrum — the method will fit these to non-oligonucleotide peaks, showing the locations of any impurities.
then impurities will not be identified: the sparse Richardson-Lucy algorithm will try to fit oligonucleotide fragments to every peak in the spectrum, even ones that correspond to fragments not from the target oligonucleotide. Therefore we also include ‘dummy’ fragments corresponding to single peaks in the spectrum — the method will fit these to non-oligonucleotide peaks, showing the locations of any impurities.
Results
For a mass spectrum from a sample containing a synthetic oligonucleotide, we generated a library of oligonucleotide and dummy fragments as described above, and applied the sparse Richardson-Lucy algorithm. Below, the model fit is plotted alongside the (smoothed, binned) spectrum and the ten most abundant fragments as estimated by the model. These fragments are represented as bars with binned m/z at the peak fragment intensity, and are separated into oligonucleotide fragments and dummy fragments indicating possible impurities. All intensities and abundances are Anscombe transformed ( ) for clarity.
) for clarity.
As the oligonucleotide in question is proprietary, its specific composition and fragmentation is not mentioned here, and the bins plotted have been transformed (without changing the shape of the data) so that individual fragment m/z values are not identifiable.
We see the data is fit extremely closely, and that the spectrum is quite clean: there is one very pronounced peak roughly in the middle of the m/z range. This peak corresponds to one of the oligonucleotide fragments in the library, although there is also an abundant dummy fragment slightly to the left inside the main peak. Fragment intensities in the library matrix are smoothed, and it may be the case that the smoothing here is inappropriate for the observed peak, hence other fragments being fit at the peak edge. Investigating these effects is a target for the rest of the project.
We also see several smaller peaks, most of which are modelled with oligonucleotide fragments. One of these peaks, at approximately bin 5352, has a noticeably worse fit if excluding dummy fragments from the library matrix (see below). Using dummy fragments improves this fit and indicates a possible impurity. Going forward, understanding and quantification of these impurities will be improved by including other common fragments in the library matrix, and by grouping fragments which correspond to the same molecules.
References
[1] Junetsu Igarashi, Yasuharu Niwa, and Daisuke Sugiyama. “Research and Development of Oligonucleotide Therapeutics in Japan for Rare Diseases”. In: Future Rare Diseases 2.1 (Mar. 2022), FRD19.
[2] Karishma Dhuri et al. “Antisense Oligonucleotides: An Emerging Area in Drug Discovery and Development”. In: Journal of Clinical Medicine 9.6 (6 June 2020), p. 2004.
[3] Catherine J. Mummery et al. “Tau-Targeting Antisense Oligonucleotide MAPTRx in Mild Alzheimer’s Disease: A Phase 1b, Randomized, Placebo-Controlled Trial”. In: Nature Medicine (Apr. 24, 2023), pp. 1–11.
[4] Benjamin D. Boros et al. “Antisense Oligonucleotides for the Study and Treatment of ALS”. In: Neurotherapeutics: The Journal of the American Society for Experimental NeuroTherapeutics 19.4 (July 2022), pp. 1145–1158.
[5] Ingvar Eidhammer et al. Computational Methods for Mass Spectrometry Proteomics. John Wiley & Sons, Feb. 28, 2008. 299 pp.
[6] Harri Lönnberg. Chemistry of Nucleic Acids. De Gruyter, Aug. 10, 2020.
[7] S. A. McLuckey, G. J. Van Berkel, and G. L. Glish. “Tandem Mass Spectrometry of Small, Multiply Charged Oligonucleotides”. In: Journal of the American Society for Mass Spectrometry 3.1 (Jan. 1992), pp. 60–70.
[8] Scott A. McLuckey and Sohrab Habibi-Goudarzi. “Decompositions of Multiply Charged Oligonucleotide Anions”. In: Journal of the American Chemical Society 115.25 (Dec. 1, 1993), pp. 12085–12095.
[9] Mario Bertero, Patrizia Boccacci, and Valeria Ruggiero. Inverse Imaging with Poisson Data: From Cells to Galaxies. IOP Publishing, Dec. 1, 2018.
[10] Elad Shaked, Sudipto Dolui, and Oleg V. Michailovich. “Regularized Richardson-Lucy Algorithm for Reconstruction of Poissonian Medical Images”. In: 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro. Mar. 2011, pp. 1754–1757.

 The morning started with four ten-minute research talks from Compass students. First was Rahil Morjaria‘s talk on “Group Testing” which explored current developments in the field, including algorithms and information-theoretic limits.
The morning started with four ten-minute research talks from Compass students. First was Rahil Morjaria‘s talk on “Group Testing” which explored current developments in the field, including algorithms and information-theoretic limits. Student Lightning Talks
Student Lightning Talks This year’s conference panel, chaired by Compass CDT Director, Professor Nick Whiteley, offered an engaging look into the professional journeys of Compass alumni Dominic Owens, Jake Spiteri and Michael Whitehouse since completing their PhDs. With shared experiences in finance, each panelist provided unique insights into the early career landscape and the skills that helped them succeed.
This year’s conference panel, chaired by Compass CDT Director, Professor Nick Whiteley, offered an engaging look into the professional journeys of Compass alumni Dominic Owens, Jake Spiteri and Michael Whitehouse since completing their PhDs. With shared experiences in finance, each panelist provided unique insights into the early career landscape and the skills that helped them succeed. The conference concluded with an enlightening special guest lecture by Professor Aline Villavicencio, Director of the Institute for Data Science and Artificial Intelligence at the University of Exeter. Her talk, “Testing the Idiomatic Language Limits of Foundation Models: The Strange Case of the Idiomatic Eager Beaver in Cloud Nine,” offered a fascinating counterpoint to the current enthusiasm surrounding LLMs.
The conference concluded with an enlightening special guest lecture by Professor Aline Villavicencio, Director of the Institute for Data Science and Artificial Intelligence at the University of Exeter. Her talk, “Testing the Idiomatic Language Limits of Foundation Models: The Strange Case of the Idiomatic Eager Beaver in Cloud Nine,” offered a fascinating counterpoint to the current enthusiasm surrounding LLMs. The successful day of talks, poster sessions and networking culminated with Professor Whiteley sharing his thoughts on what we learned throughout the event. He concluded that the future of our field is certain to be exciting and will encompass a huge range of different areas and ideas. This year’s conference embodied this by providing a platform for students, academics, and industry professionals to share new insights from many different sectors, and to form strong relationships to help forge a path to the future of data science.
The successful day of talks, poster sessions and networking culminated with Professor Whiteley sharing his thoughts on what we learned throughout the event. He concluded that the future of our field is certain to be exciting and will encompass a huge range of different areas and ideas. This year’s conference embodied this by providing a platform for students, academics, and industry professionals to share new insights from many different sectors, and to form strong relationships to help forge a path to the future of data science.






