A post by Conor Crilly, PhD student on the Compass programme.

Introduction

This project investigates uncertainty quantification methods for expensive computer experiments. It is supervised by Oliver Johnson of the University of Bristol, and is partially funded by AWE.

Outline

Physical systems and experiments are commonly represented, albeit approximately, using mathematical models implemented via computer code. This code, referred to as a simulator, often cannot be expressed in closed form, and is treated as a ‘black-box’. Such simulators arise in a range of application domains, for example engineering, climate science and medicine. Ultimately, we are interested in using simulators to aid some decision making process. However, for decisions made using the simulator to be credible, it is necessary to understand and quantify different sources of uncertainty induced by using the simulator. Running the simulator for a range of input combinations is what we call a computer experiment [1]. As the simulators of interest are expensive, the available data is usually scarce. Emulation is the process of using a statistical model (an emulator) to approximate our computer code and provide an estimate of the associated uncertainty.

Intuitively, an emulator must possess two fundamental properties

It must be cheap, relative to the code
It must provide an estimate of the uncertainty in its output

A common choice of emulator is the Gaussian process emulator, which is discussed extensively in [2] and described in the next section.

Types of Uncertainty

There are many types of uncertainty associated with the use of simulators including input, model and observational uncertainty. One type of uncertainty induced by using an expensive simulator is code uncertainty, described by Kennedy and O’Hagan in their seminal paper on calibration [3]. To paraphrase Kennedy and O’Hagan: In principle the simulator encodes a relationship between a set of inputs and a set of outputs, which we could evaluate for any given combination of inputs. However, in practice, it is not feasible to run the simulator for every combination, so acknowledging the uncertainty in the code output is required.

Gaussian Processes

Suppose we are interested only in investigating code uncertainty, that is, we simply want to predict the code output for some untried combinations of control inputs. We denote our simulator by $f(\cdot)$ , such that $f: \mathcal{X} \mapsto \mathcal{Y}$ . For simplicity, we take $\mathcal{X} \equiv \mathbb{R}$ and $\mathcal{Y} \equiv \mathbb{R}$ , although the methods described can easily be adapted to more general spaces.

Treating our code $f(\cdot)$ as unknown, a useful way to model $f(\cdot)$ is to adopt a Bayesian approach and use a random function model [4]. In our case, we use a Gaussian process ( $\mathcal{GP}$ ) as a prior for $f(\cdot)$ , and our ultimate aim will be to derive a posterior distribution which we will use to make predictions at new test inputs. Interpreting our $\mathcal{GP}$ as a prior for $f(\cdot)$ is intuitive, and useful, since we can subtly tweak the form of our $\mathcal{GP}$ to incorporate our prior knowledge about the shape of $f(\cdot)$ . Specifically, we can alter the kernel and mean functions of the $\mathcal{GP}$ . Loosely speaking a $\mathcal{GP}$ can be viewed as an `infinite dimensional version’ of a multivariate Gaussian. A $\mathcal{GP}$ can be defined as follows

Definition 1: A Gaussian process is a collection of random variables, any finite combination of which have a multivariate Gaussian distribution.

Analogously to a multivariate Gaussian, which is fully specified by its mean $\mu$ and covariance matrix $\Sigma$ , a $\mathcal{GP}$ is fully specified by its mean function $m(x)$ and covariance function, $k(x,x')$ .

A $\mathcal{GP}$ prior on a function $f$ is then written as

$f(x) \sim \mathcal{GP}(m(x), k(x,x')).$

**Figure 1: (Left)** An illustration of Definition 1, with indices x = 0 and x = 1. The value of f(x) at each index can take any value along the blue line, although its location is distributed according to a standard univariate Gaussian and can thus take any value in R. **(Right)** Imagine making the same argument for every point x ∈R, as we made for x ∈{0,1} in the left-hand plot. This is what we have done on the right; the dashed line corresponds to the mean, whilst the grey shading corresponds to two standard deviations from the mean.

Prior

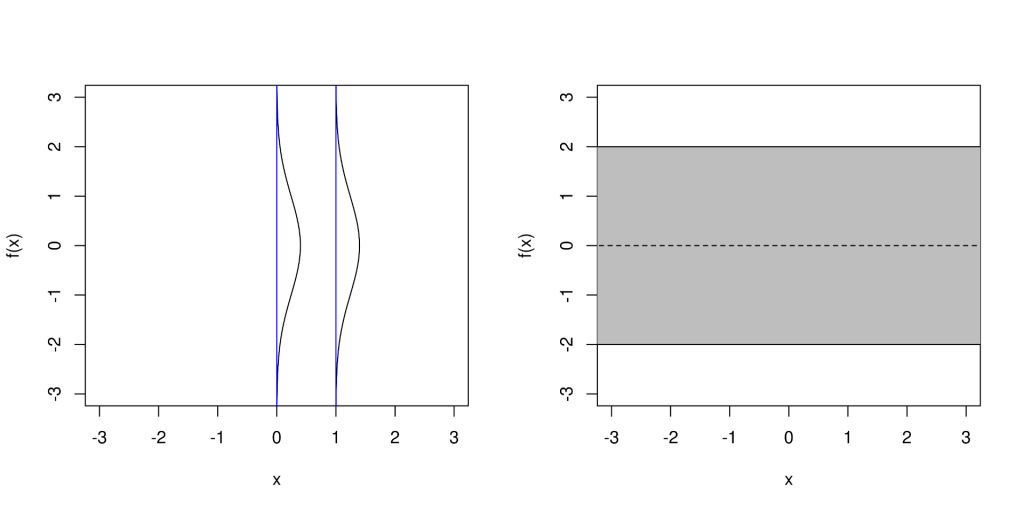
To clarify how Definition 1 relates to emulation of our simulator, the random variables in Definition 1 correspond to the values of the function $f(\cdot)$ we want to emulate, and the argument assumes the role of the index. Definition 1 then defines the relationship between all of these values in terms of finite subsets thereof. We can easily visualise draws from a $\mathcal{GP}$ prior with one dimensional input and output spaces, just as we have done in Figure 2, using the following steps.

Choose your favourite index points $x_1 < x_2 < \dots < x_N\, \in \mathbb{R}$
Choose your mean function $\mu(\cdot)$ and kernel function $k(\cdot,\cdot)$ , specifying any hyperparameters
Calculate the covariance matrix $\Sigma$ , where $\Sigma_{ij} = k(x_i,x_j)$
By definition, $\Sigma$ is positive definite so we can decompose $\Sigma$ such that $\Sigma = \Gamma\Gamma^{T}$
Simulate an $N$ dimensional vector $f$ according to $f = \mu + \Gamma \mathcal{N}(0, I_{N \times N})$ , where $\mu_i = \mu(x_i)$
Plot each of the points $(x_i, f_i)$

Posterior

Suppose we are interested in emulating some function. For illustration we can simulate some `toy’ data from the function $f(x) = \frac{3}{2}(\sin(\frac{x}{3}) + \cos(\frac{x}{3}))$ . With noise free observations, as in a computer experiment, the posterior process is easily derived. According to our $\mathcal{GP}$ prior, the joint distribution of the function values $f_{te}$ at the test and $f_{tr}$ at the training inputs is multivariate Gaussian, so to obtain the posterior we can simply condition the test outputs on the observed training outputs, giving us another Gaussian with the following posterior mean and covariance

$\bar{f}_{te} = \Sigma(x_{te}, x_{tr})\Sigma(x_{tr}, x_{tr})^{-1}f_{tr}$
$\Sigma_{te} = \Sigma(x_{te}, x_{te}) - \Sigma(x_{te}, x_{tr})\Sigma(x_{tr}, x_{tr})^{-1}\Sigma(x_{tr}, x_{te})$

With minor adjustments the same process as we used for the prior can be used to draw `functions’ from the posterior, $\mathcal{N}(\bar{f}_{te}, \Sigma_{te})$ . See Figure 2 for an illustration of this.

This simple conditioning procedure also works if we assume that observations are made with some additive Gaussian noise. However, when our likelihood is non-Gaussian, for example when using Gaussian processes for classification, difficulties arise. In particular, our posterior is no longer Gaussian and its derivation involves intractable integrals; $\mathcal{GP}$ s with non-Gaussian likelihoods is an active area of research [5].

**Figure 2: (Left)** Three ‘functions’ drawn from a GP prior with zero mean function and squared exponential kernel function. **(Right)** Three ‘functions’ drawn from the corresponding posterior distribution, with noiseless training data simulated from f(x) (defined in the section above on the posterior) at x ∈ {−2,−1,1,1.5}. Each of the functions and the posterior mean (dashed line) interpolate the training data with uncertainty quantification (two standard deviations in grey) provided by the posterior variance. Uncertainty is zero at the training points and increases as we move further away from them.

Constrained GPs

Standard $\mathcal{GP}$ regression is interesting, but what if we have some specific prior knowledge about the function we want to emulate? Perhaps we know that the function is monotone or convex. How can we incorporate this knowledge into our model to improve the emulator?

Notice that both monotonicity and convexity of a function can be specified in terms of derivatives thereof. One useful theorem is that $\mathcal{GP}s$ are closed under linear transformation [2]. That is, if $f$ is a $\mathcal{GP}$ , and $\mathcal{L}$ is a linear operator, the result, $\mathcal{L}f$ , is also a $\mathcal{GP}$ . Indeed, we can make inference about both function values and derivative values using the joint $\mathcal{GP}$ , $(f, \mathcal{L}f)$ , by applying the standard $\mathcal{GP}$ regression we just introduced.

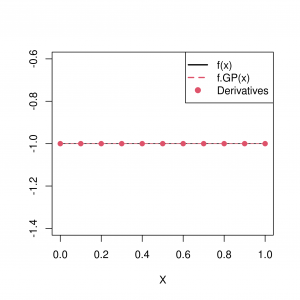
This approach is only useful if we actually observe the derivatives (equality constraints), and we illustrate in Figure 3 how this can improve emulation of the function $f(x) = -\frac{1}{8}\big((2x -1)^2 -1\big)$ [8]. Note further that linear differential equations are linear combinations of differential operators and are thus still linear operators. This allows us to apply this technique to estimate functions with `differential equation constraints’, as occur in physical settings [6].

Several approaches have been proposed in the literature to tackle the case where we do not observe the derivatives, which would be the case if we could only assume monotonicity [7]. In [7], indicator variables are used at predefined inputs to indicate whether or not the derivative is positive. Inference is then made conditional on these indicator variables. One issue with this approach is that sample paths are not guaranteed to obey the desired constraints at all points in the domain $\mathcal{X}$ . However, an alternative approach discussed in [6] circumvents this issue, enforcing constraints continuously.

**Figure 3: (Left)** Standard GP regression – we plot the true function, posterior mean and the uncertainty. Training points were simulated randomly on [0.2,0.8] and the uncertainty (two standard deviations) grows quickly outside of this interval. **(Right)** We now include derivatives at locations simulated randomly on [0,1] (yellow). These improve the uncertainty quantification outside of [0.2,0.8] significantly.

The derivative process, the posterior mean of the derivative process and the values of the derivatives used as training points. The posterior mean interpolates the observed derivatives.

Conclusion

This was a brief introduction to $\mathcal{GP}$ s and their role within emulation. We discussed the simple case of $\mathcal{GP}$ regression with noiseless observations (and observations with additive Gaussian noise) and the inclusion of linear operator constraints. Training this model is relatively straightforward and can be done so via maximum-likelihood estimation. More complex models are often considerably harder to train due to the presence of intractable integrals. However, this can be tackled using MCMC methods.

References

[1] J. Sacks, W. J. Welch, T. J. Mitchell, and H. P. Wynn. Design and analysis of computer experiments. Statistical Science, 4(4):409–423, Nov 1989.

[2] C. E. Rasmussen and C. K. I. Williams. Gaussian Processes For Machine Learning. The MIT Press, Cambridge 2006.

[3] M. C. Kennedy and A. O’Hagan. Bayesian calibration of computer models. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 63(3):425–464, 2001.

[4] T. J. Santner, B. J. Williams, and W. I. Notz. The Design and Analysis of Computer Experiments. Springer Series in Statistics. Springer, 2003.

[5] ST John. Gaussian processes for non-gaussian likelihoods. Gaussian Process Summer School 2021. http://gpss.cc/gpss21/slides/John2021.pdf.

[6] C. Jidling, N. Wahlström, A. Wills, and T. B. Schön. Linearly constrained gaussian processes. In Advances in Neural Information Processing Systems, volume 30. Curran Associates, Inc., 2017.

[7] S. Golchi, D. R. Bingham, H. Chipman, and D. A. Campbell. Monotone emulation of computer experiments. SIAM/ASA Journal on Uncertainty Quantification, 3(1):370–392, Jan 2015.

[8] L. Swiler, M. Gulian, A. Frankel, C. Safta, and J. Jakeman. A survey of constrained gaussian process regression: Approaches and implementation challenges. Journal of Machine Learning for Modeling and Computing, 1(2):119–156, 2020. ISSN 2689-3967. doi: 10.1615/JMachLearnModelComput.2020035155.