A post by Emerald Dilworth, PhD student on the Compass programme.
This blog post serves as an accessible introduction to Graph Neural Networks (GNNs). An overview of what graph structured data looks like, distributed vector representations, and a quick description of Neural Networks (NNs) are given before GNNs are introduced.
An Introductory Overview of GNNs:
You can think of a GNN as a Neural Network that runs over graph structured data, where we know features about the nodes – e.g. in a social network, where people are nodes, and edges are them sharing a friendship, we know things about the nodes (people), for instance their age, gender, location. Where a NN would just take in the features about the nodes as input, a GNN takes in this in addition to some known graph structure the data has. Some examples of GNN uses include:
- Predictions of a binary task – e.g. will this molecule (which the structure of can be represented by with a graph) inhibit this given bacteria? The GNN can then be used to predict for a molecule not trained on. Finding a new antibiotic is one of the most famous papers using GNNs [1].
- Social networks and recommendation systems, where GNNs are used to predict new links [2].
What is a Graph?
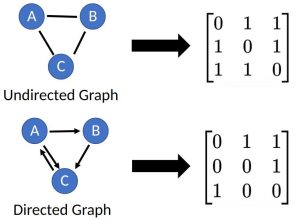
A graph, , is a data structure that consists of a set of nodes,
, and a set of edges,
. Graphs are used to represent connections (edges) between objects (nodes), where the edges can be directed or undirected depending on whether the relationships between the nodes have direction. An
node graph can be represented by an
matrix, referred to as an adjacency matrix.
Idea of Distributed Vector Representations
In machine learning architectures, the data input often needs to be converted to a tensor for the model, e.g. via 1-hot encoding. This provides an input (or local) representation of the data, which if we think about 1-hot encoding creates a large, sparse representation of 0s and 1s. The input representation is a discrete representation of objects, but lacks information on how things are correlated, how related they are, what they have in common. Often, machine learning models learn a distributed representation, where it learns how related objects are; nodes that are similar will have similar distributed representations. (more…)

