Category: Students

Student Perspectives: Machine Learning Models for Probability Distributions

Posted on by th17628

A post by Tennessee Hickling, PhD student on the Compass programme.


Introduction
Probabilistic modelling provides a consistent way to deal with uncertainty in data. The central tool in this methodology is the probability distribution, which describes the randomness of observations. To create effective models of reality, we need to be able to specify probability distributions that are flexible enough to capture real phenomena whilst remaining feasible to estimate. In the past decade machine learning (ML) has developed many new and exciting ways to represent and learn potentially complex probability distributions.

ML has provided significant advances in modelling of high dimensional and highly structured data such as images or text. Many of these modern approaches are applied as “generative models”. The goal of such approaches is to sample new synthetic observations from an approximate distribution which closely matches the target distribution. For example, we may use many images of cats to learn an approximate distribution, from which we can sample new images of cats that appear realistic. Usually, a “generative model” indicates the requirement to sample from the model, but not necessarily assign probabilities to observed data. In this case, the model captures uncertainty by imitating the structure and randomness of the data.

Many of these modern methods work by transforming simple randomness (such as a Normal distribution) into the target complex randomness. In my own research, I work on a known limitation of such approaches to replicate a particular aspect of randomness – the tails of probability distributions [1, 11]. In this post, I wanted to take a step back and provide an overview of and connections between two ML methods that can be used to model probability distributions – Normalising Flows (NFs) and Variational Autoencoders (VAEs).

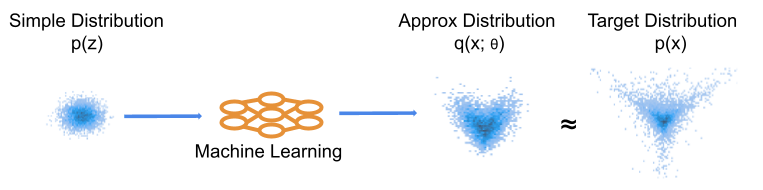
Figure 1: Basic illustration of ML learning of a distribution. We optimise the machine learning model to produce a distribution close to our target. This is often conceptualised in the generative direction, such that our ML model moves samples from the simple distribution to more closely match the target observations.

Some Background
Consider real valued vectors $z \in \mathbb{R}^{d_z}$ and $x \in \mathbb{R}^{d_x}$. In this post I mirror notation used in [2], where $p(x)$ refers to the density and distribution of $x$ and $x \sim p(x)$ indicates samples according to that distribution. The generic set up I am considering is that of density estimation – trying to model the distribution $p(x)$ of some observed data $\{x_i\}_{i=1}^{N}$. I use a semicolon to denote parameters, so $p(x; \beta)$ is a distribution over $x$ with parameters $\beta$. I also make use of different letters to distinguish different distributions, for example using $q(x)$ to denote an approximation to $p(x)$. The notation $\mathbb{E}_p[f(x)]$ refers to the standard expectation of $f(x)$ over the distribution $p$.

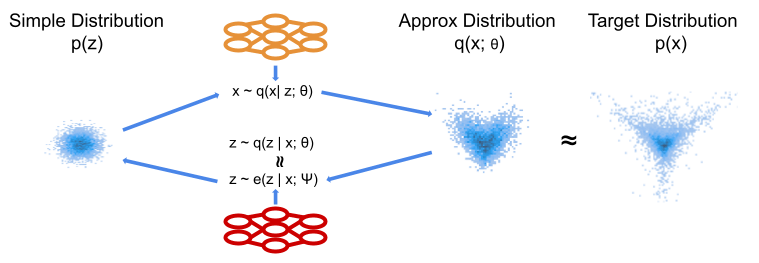
The discussed methods introduce some simple source of randomness arising from a known, simple latent distribution $p(z)$. This is also referred to in some literature as the prior, though the usage is not straightforwardly relatable to traditional Bayesian concepts. The goal is then to fit an approximate $q(x|z; \theta)$, that is a conditional distribution, such that $$q(x; \theta) = \int q(x|z; \theta)p(z)dz \approx p(x),$$in words, the marginal density over $x$ implied by the conditional density, is close to our target distribution $p(x)$. In general, we can’t compute $q(x)$, as we can’t solve the above integral for very flexible $q(x | z; \theta)$.

Variational Inference
We commonly make use of the Kullback-Leibler (KL) divergence, which can be interpreted as measuring the difference between two probability distributions. It is a useful practical tool, since we can compute and optimise the quantity in a wide variety of situations. Techniques which optimise a probability distribution using such divergences are known as variational methods. There are other choices of divergence, but KL is the most standard. Important properties of KL are that the quantity $KL(p|| q)$ is non-negative and non-symmetric i.e. $KL(p|| q) \neq KL(q || p)$.

Given this, we can see that a natural objective is to minimise the difference between distributions, as measured by the KL, $$KL(p(x) || q(x; \theta)) = \int p(x) \log \frac{p(x)}{q(x; \theta)} dx.$$Advances in this area have mostly developed new ways to make this optimisation tractable for flexible $q(x | z; \theta)$.

Normalising Flow
A normalising flow is a parameterised transformation of a random variable. The key simplifying assumption is that the forward generation is deterministic. That is, for $d_x = d_z$, that $$
x = T(z; \theta),$$for some transformation function $T$. We additionally require that $T$ is a differentiable bijection. Given these requirements, we can express the approximate density of $x$ exactly as $$q_x(x; \theta) = p_z(T^{-1}(x; \theta))\big|\text{det } J_{T^{-1}}(x; \theta)\big|.$$Here, $\text{det }J_{T^{-1}}$ is the determinant of the Jacobian of the inverse transformation. Research on NFs has developed numerous ways to make the computation of the Jacobian term tractable. The standard approach is to use neural networks to produce $\theta$ (the parameters of the transformation), with numerous ways of configuring the model to capture dependency between dimensions. Additionally, we often stack many layers to provide more flexibility. See [10] and the review [2] for more details on how this is achieved.

As we have access to an analytic approximate density, we can minimise the negative log-likelihood of our model, $$\mathcal{J}(\theta) = -\sum_{i=1}^{N} \log q(x_i; \theta),$$which is the Monte-Carlo approximation of the KL loss (up to an additive constant). This is straightforward to optimise using stochastic gradient descent [9] and automatic differentiation.

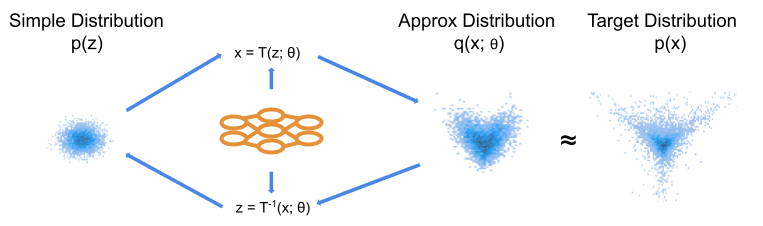
Figure 2: Schematic of NF model. The ML model produces the parameters of our transformation, which are identical in the forward and backwards directions. We choose the transformation such that we can express an analytic density function for our approximate distribution.

Variational Autoencoder
In the Variational Autoencoder (VAE) [3] the conditional distribution $q(x| z; \theta)$ is known as the decoder. VAEs consider the marginal in terms of the posterior, that is $$q(x; \theta) = \frac{q(x | z; \theta)p(z)}{q(z | x; \theta)}.$$The posterior $q(z | x; \theta)$ is itself not generally tractable. VAEs proceed by introducing an encoder, which approximates $q(z | x; \theta)$. This is itself simply a conditional distribution $e(z | x; \psi)$. We use this approximation to express the log marginal over $x$ as below.
$$\begin{align}
\log q(x; \theta) &= \mathbb{E}_{e}\bigg[\log q(x; \theta)\frac{e(z | x; \psi)}{e(z | x; \psi)}\bigg] \\
&= \mathbb{E}_{e}\bigg[\log\frac{q(x | z; \theta)p(z)}{q(z | x; \theta)}\frac{e(z | x; \psi)}{e(z | x; \psi)}\bigg] \\
&= \mathbb{E}_{e}\bigg[\log\frac{q(x | z; \theta)p(z)}{e(z | x; \psi)}\bigg] + KL(e(z | x; \psi) || q(z | x; \theta)) \\
&= \mathcal{J}_{\theta,\psi} + KL(e(z | x; \psi) || q(z | x; \theta))
\end{align}$$
The additional approximation gives a more complex expression and does not provide an analytical approximate density. However, as $KL(e(z | x; \psi) || q(z | x; \theta))$ is positive, $\mathcal{J}_{\theta,\psi}$ forms a lower bound on $\log q(x; \theta)$. This expression is commonly referred to as the Evidence Lower Bound (or ELBO). The second term, the divergence between our encoder and the implied posterior will be minimised as we increase $\mathcal{J}_{\theta,\psi}$ in $\psi$. As we increase $\mathcal{J}_{\theta,\psi}$, we will either be increasing $\log q(x; \theta)$ or reducing $KL(e(z | x; \psi) || q(z | x; \theta))$.

The goal is to increase $\log q(x; \theta)$, which we hope occurs as we optimise over both parameters. This ambiguity in optimisation results in well known issues, such as posterior collapse [12] and can result in some counter-intuitive behaviour [4]. Despite this, VAEs remain a powerful and popular approach. An important benefit is that we no longer require $d_x = d_z$, which means we can map high dimensional $x$ to low dimensional $z$ to perform dimensionality reduction.

Figure 3: Schematic of VAE model. We now have a stochastic forward transformation. To optimise this we introduce a decoder model which approximates the posterior implied by the forward transformation. We now have a more flexible transformation, but two models to train and no analytic approximate density.

Surjective Flows
We can now identify a connection between NFs and VAEs. Recent work has reinterpreted NFs within the VAE framework, permitting a broader class of transitions whilst retaining analytic tractability of NFs [5]. Considering our decoding conditional as $$q(x|z; \theta) = \delta(x – T(z; \theta)),$$ we have the posterior exactly as
$$q(z|x; \theta) = \delta(z – T^{-1}(x; \theta)),$$
where $\delta$ is the dirac delta function.

This provides a view of a NF as a special case of a VAE, where we don’t need to approximate the posterior. Considering our VAE approximation, $$
\log q(x; \theta) = \mathbb{E}_e\big[\log p(z) + \log\frac{q(x | z; \theta)}{e(z | x; \psi)}\big] + KL(e(z | x; \psi) || q(z | x; \theta)),
$$and taking $e(z | x; \psi) = q(z | x; \theta)$, then the final KL term is 0 by definition. In that case, we recover our analytic density for NFs (see [5] for details).

Note that accessing an analytic density depends on having $e(z | x; \psi) = q(z | x; \theta)$ and computing $$\mathbb{E}_e\big[\log p(z) + \log\frac{q(x | z; \theta)}{e(z | x; \psi)}\big].$$These requirements are actually weaker than those we apply in the case of standard NFs. Consider a deterministic transformation $T^{-1}(x)$ which is surjective, crucially we can have many $x$ which map to the same $z$, so no longer have an analytic inverse. However we can still choose a $q(x | z)$ which is stochastic inverse of $T^{-1}$. For example, consider an absolute value surjection, $q(z | x) = \delta(z – |x|)$, to invert this transformation we can choose $q(x | z) = \frac{1}{2}\delta(x – z) + \frac{1}{2}\delta(x + z)$, which we can sample from straight-forwardly. This transformation enforces symmetry across the origin in the approximate distribution, a potentially useful inductive bias. In this example, and many others, we can also compute the density exactly. This has led to a number of interesting extensions to NFs, such as “funnel flows” which have $d_z < d_x$ but retain an analytic approximate density [6]. As we retain an analytic approximate density, we can optimise them in the same way as NFs.

Figure 4: Schematic of a surjective transformation. We have a stochastic forward transformation, but the inverse is deterministic. This restricts what transformations we can have, but retains an analytic approximate density.

Conclusion
I have presented an overview of two widely-used methods for modelling probability distributions with machine learning techniques. I’ve also highlighted an interesting connection between these methods, an area of research that has led to the development of interesting new models. It’s worth noting that other important classes of ML models such as Generative Adversarial Networks and Diffusion models can also be interpreted as approximate probability distributions. There are many superficial connections between those methods and the ones discussed here. Exploring these theoretical similarities presents an compelling direction of research to sharpen understanding of such models’ relative advantages. Another promising direction is the synthesis of these methods, where researchers aim to harness the strengths of each approach [7,8]. This not only enhances the existing knowledge base but also offers opportunities for innovative applications in the field.

References
[1] Jaini, Priyank, et al. “Tails of Lipschitz triangular flows.” International Conference on Machine Learning. PMLR, 2020
[2] Papamakarios, G., et al. “Normalizing flows for probabilistic modeling and inference.” Journal of Machine Learning Research, 2021
[3] Kingma, Diederik P., and Max Welling. “Auto-encoding variational bayes.” arXiv:1312.6114, 2013
[4] Rainforth, Tom, et al. “Tighter variational bounds are not necessarily better.” International Conference on Machine Learning. PMLR, 2018
[5] Nielsen, Didrik, et al. “Survae flows: Surjections to bridge the gap between vaes and flows.” Advances in Neural Information Processing, 2020
[6] Samuel Klein, et al. “Funnels: Exact maximum likelihood with dimensionality reduction.” arXiv:2112.08069, 2021
[7] Kingma, Durk P., et al. “Improved variational inference with inverse autoregressive flow.” Advances in neural information processing systems , 2016
[8] Zhang, Qinsheng, and Yongxin Chen. “Diffusion normalizing flow.” Advances in Neural Information Processing Systems 34, 2021
[9] Ettore Fincato “An Introduction to Stochastic Gradient Methods” https://compass.blogs.bristol.ac.uk/2023/03/14/stochastic-gradient-methods/
[10] Daniel Ward “An introduction to normalising flows” https://compass.blogs.bristol.ac.uk/2022/07/13/2608/
[11] Tennessee Hickling and Dennis Prangle, “Flexible Tails for Normalising Flows, with Application to the Modelling of Financial Return Data”, 8th MIDAS Workshop, ECML PKDD, 2023
[12] Lucas, James, et al. “Don’t blame the elbo! a linear vae perspective on posterior collapse.” Advances in Neural Information Processing Systems 32, 2019

Student perspectives: Compass Annual Conference 2023

Posted on by dominic.broadbent

A post by Dominic Broadbent, PhD student on the Compass CDT, and Michael Whitehouse, PhD student of the Compass CDT (recently submitted thesis)

Introduction

September saw the second annual Compass Conference, hosted in the Fry Building, the home of the School of Mathematics. The event was particularly special as it is the first time that all five Compass cohorts were brought together, and it was a fantastic opportunity to celebrate the achievements and research of the Compass CDT with external partners.  This year the theme was “Communicating Research in Context“, focusing on how research can be better communicated, and the need to highlight the motivation and applications of mathematical research.

Research talks

The day began with four long form talks touching on the topic of communicating research. Starting with Alessio Zakaria’s talk which delved into Hypothesis tests, commenting on their criticial role as the defacto statistical tool across the sciences, and how p-hacking has led to a replication crisis that undermines public confidence in research. The next talk by Sam Stockman and Emerald Dilworth discussed the challenges they faced, and the key takeaways from their shared experience of communicating mathematics with researchers in the geographical sciences. Following this, Ed Davis’s interactive talk “The Universal Language of Visualisations” explored how effective visualisation techniques should differ by the intended audience, with examples from his research and activities outside of academia. The last talk by Dan Milner explored his research on understanding the effect of environmental factors on outcomes of smallholder farmers in Kenya. He took us through the process of collecting data on the ground, to modelling and communicating results to external partners.  After each talk there was an opportunity to ask questions, allowing for audience participation and the sparking of interesting discussions. The format mirrored that which is most frequently used in external academic conferences, giving the speakers a chance to practice their technique in front of friendly faces.

Lightning talks

After a short break, we jumped back into the fray with a series of 3-minute fast-paced lightning talks. A huge range of topics were covered, all the way from developing modelling techniques for the electric grid of the future, to predicting the incidence of Cerebral Vasospasm at the Southmead Hospital ICU. With such a short time to present, these talks were a great exercise in distilling research into just the essentials, knowing there is very limited time to garner the audience’s interest and convey an effective message.

Special guest lecture

After lunch, we reconvened to attend the special guest lecture. The talk, entitled Bridging the gap between research and industry, was delivered by Ruth Voisey, CEO of the Smith institute. It outlined Ruth’s journey from writing her PhD thesis ‘Multiple wave scattering by quasiperiodic structures’, to CEO of the Smith Institute – via an internship with the acoustic research team at Dyson. It was particularly refreshing to hear Ruth’s candid account of her ‘non-linear’ rise to CEO, accrediting her success to strong principles of clear research communication and ‘mathematical evangelicalism’.

As PhD students in the bubble of academia, the path to opportunities in the world of industry can often feel clouded – Ruth’s lecture painted a clear picture of how one can transition from university based research to a rewarding career outside of this bubble, applying such research to tangible problems in the real world. 

Panel discussion and poster session

The special guest lecture was followed by a discussion on communicating research in context, with panel members Ruth Voisey, David Greenwood, Helen Barugh, Oliver Johnson, plus Compass CDT students Ed Davis and Sam Stockman. The panel discussed the difficulty of communicating the nuances of research conclusions with the public, with a particular focus on handling these nuances when talking to journalists – stressing the importance of communicating the limitations of the research in question.

This was followed by a poster session, one enthusiastic student had the following comment “it was great to see of all the Compass students’ hard work being celebrated and shared with the wider data science community”.

Concluding remarks

To cap off the successful event, Compass students Hannah Sansford and Josh Givens delivered some concluding remarks which were drawn from comments made by students about what key points they’d taken from the day. These focused on the importance of clear communication of research throughout the whole pipeline, from inception in discussion with fellow academics to the dissemination of knowledge to the general population.

The day ended with a walk to Goldney Hall, where students, staff, and attendees enjoyed delicious food, wine, and access to the beautiful Orangery gardens.

2023/24 Compass research projects confirmed

Posted on by harriet.lee

Our Cohort 4 Compass students have confirmed their PhD projects for the next 3 years and are establishing the direction of their own research within the CDT.

 

Supervised by the Institute for Statistical Science:

Qi Chen:  Methodology for inferring directed graphs representing generative processes      Supervised by Dan Lawson

Emma Ceccherini:  Covariate Information for Dynamic Network Embedding.  Supervised by Ian Gallagher & Dan Lawson

Henry Bourne: Investigating the Effect of Latent Representations on Continual Learning Performance.  Supervised by Rihuan Ke

Rachel Wood:  Comparing qualitatively different data at scale.  Supervised by Dan Lawson

Dylan Dijk:  Robust estimation and inference for high-dimensional time series.  Supervised by Haeran Cho

Rahil Morjaria:  New Directions in Group Testing.  Supervised by Sid Jaggi

Xinrui Shi:  Collective decision making in distributed systems.  Supervised by Ayalvadi Ganesh

 

The following projects are supervised in collaboration with the Institute for Statistical Science (IfSS) and our other internal partners at the University of Bristol:

Codie Wood:  Misclassification in binary and categorical variables: development of methods and software for epidemiology.  Supervised by Kate Tilling & Rachael Hughes from Bristol Medical School (Population Health Science).  Plus Jonathan Bartlett (London School Hygiene Tropical Medicine)

Ben Anson:  Graph deep kernel machines. Supervised by Laurence Aitchison (Department of Computer Science)

Sam Bowyer:  Fast and correct Bayesian inference with massively parallel methods. Supervised by Laurence Aitchison (Department of Computer Science)

Sam Perren:  Validity of population adjustment methods for disconnected networks of evidence.  Supervised by Nicky Welton, David Phillippo & Hugo Pedder from Bristol Medical School (Population Health Science)

Emma Tarmey:   Variable selection in causal inference: development of methods and software for epidemiology.  Kate Tilling & Jonathan Sterne from Bristol Medical School (Population Health Science).  Plus Rhian Daniel (Cardiff University)

 

 

Student Perspectives: Density Ratio Estimation with Missing Data

Posted on by josh.givens

A post by Josh Givens, PhD student on the Compass programme.

Density ratio estimation is a highly useful field of mathematics with many applications.  This post describes my research undertaken alongside my supervisors Song Liu and Henry Reeve which aims to make density ratio estimation robust to missing data. This work was recently published in proceedings for AISTATS 2023.

Density Ratio Estimation

Definition

As the name suggests, density ratio estimation is simply the task of estimating the ratio between two probability densities. More precisely for two RVs (Random Variables) Z^0, Z^1 on some space \mathcal{Z} with probability density functions (PDFs) p_0, p_1 respectively, the density ratio is the function r^*:\mathcal{Z}\rightarrow\mathbb{R} defined by

r^*(z):=\frac{p_0(z)}{p_1(z)}.

Plot of the scaled density ratio alongside the PDFs for the two classes.

Density ratio estimation (DRE) is then the practice of using IID (independent and identically distributed) samples from Z^0 and Z^1 to estimate r^*. What makes DRE so useful is that it gives us a way to characterise the difference between these 2 classes of data using just 1 quantity, r^*.

 

The Density Ratio in Classification

We now give demonstrate this characterisability in the case of classification. To frame this as a classification problem define Y\sim\text{Bernoulli}(0.5) and Z by Z|Y=y\sim Z^{y}. The task of predicting Y given Z using some function \phi:\mathcal{Z}\rightarrow\{0,1\} is then our standard classification problem. In classification a common target is the Bayes Optimal Classifier, the classifier \phi^* which maximises \mathbb{P}(Y=\phi(Z)). We can write this classifier in terms of r^*  as we know that \phi^*(z)=\mathbb{I}\{\mathbb{P}(Y=1|Z=z)>0.5\} where \mathbb{I} is the indicator function. Then, by the total law of probability, we have

\mathbb{P}(Y=1|Z=z)=\frac{p_{Z|Y=1}(z)\mathbb{P}(Y=1)}{p_{Z|Y=1}(z)\mathbb{P}(Y=1)+p_{Z|Y=0}(z)\mathbb{P}(Y=0)}

=\frac{p_1(z)\mathbb{P}(Y=1)}{p_1(z)\mathbb{P}(Y=1)+p_0(z)\mathbb{P}(Y=0)} =\frac{1}{1+\frac{1}{r}\frac{\mathbb{P}(Y=0)}{\mathbb{P}(Y=1)}}.

Hence to learn the Bayes optimal classifier it is sufficient to learn the density ratio and a constant. This pattern extends well beyond Bayes optimal classification to many other areas such as error controlled classification, GANs, importance sampling, covariate shift, and others.  Generally speaking, if you are in any situation where you need to characterise the difference between two classes of data, it’s likely that the density ratio will make an appearance.

Estimation Implementation – KLIEP

Now we have properly introduced and motivated DRE, we need to look at how we can go about performing it. We will focus on one popular method called KLIEP here but there are a many different methods out there (see Sugiyama et al 2012 for some additional examples.)

The intuition behind KLIEP is simple: as r^* \cdot p_0=p_1, if \hat r\cdot p_0 is “close” to p_1 then \hat r is a good estimate of r^*. To measure this notion of closeness KLIEP uses the KL (Kullback-Liebler) divergence which measures the distance between 2 probability distributions. We can now formulate our ideal KLIEP objective as follows:

\underset{r}{\text{min}}~ KL(p_1|p_0\cdot r)

\text{subject to:}~ \int_{\mathcal{Z}}r(z)p_0(z)\mathrm{d}z=1

where KL(p|p') represent the KL divergence from p to p'. The constraint  ensures that the right hand side of our KL divergence is indeed a PDF. From the definition of the KL-divergence we can rewrite the solution to this as \hat r:=\frac{\tilde r}{\mathbb{E}[r(X^0)]} where \tilde r is the solution to the unconstrained optimisation

\underset{r}{\text{min}}~\mathbb{E}[\log (r(Z^1))]-\log(\mathbb{E}[r(Z^0)]).

As this is now just an unconstrained optimisation over expectations of known transformations of Z^0, Z^1, we can approximate this using samples. Given samples z^0_1,\dotsc,z^0_n from Z_0 and samples z^1_1,\dotsc,z^1_n from Z_1 our estimate of the density ratio will be \hat r:=\left(\frac{1}{n}\sum_{i=1}^nr(z_i^0)\right)^{-1}\tilde r  where \tilde r solves

\underset{r}{\min}~ \frac{1}{n}\sum_{i=1}^n \log(r(z^1_i))-\log\left(\frac{1}{n}\sum_{i=1}^n r(z^0_i)\right).

Despite KLIEP being commonly used, up until now it has not been made robust to missing not at random data. This is what our research aims to do.

Missing Data

Suppose that instead of observing samples from Z, we observe samples from some corrupted version of Z, X. We assume that \mathbb{P}(\{X=\varnothing\}\cup \{X=Z\})=1 so that either X is missing or X takes the value of Z. We also assume that whether X is missing depends upon the value of Z. Specifically we assume \mathbb{P}(X=\varnothing|Z=z)=\varphi(z) with \varphi(z) not constant and refer to \varphi as the missingness function. This type of missingness is known as missing not at random (MNAR) and when dealt with improperly can lead to biased result. Some examples of MNAR data could be readings take from a medical instrument which is more likely to err when attempting to read extreme values or recording responses to a questionnaire where respondents may be more likely to not answer if the deem their response to be unfavourable. Note that while we do not see what the true response would be, we do at least get a response meaning that we know when an observation is missing.

Missing Data with DRE

We now go back to density ratio estimation in the case where instead of observing samples from  Z^0,Z^1  we observe samples from their corrupted versions X^0, X^1. We take their respective missingness functions to be \varphi_0, \varphi_1 and assume them to be known. Now let us look at what would happen if we implemented KLIEP with the data naively by simply filtering out the missing-values. In this case, the actual density ratio we would be estimating would be

r'(z):=\frac{p_{X_1|X_1\neq\varnothing}(z)}{p_{X_0|X_o\neq\varnothing}(z)}\propto\frac{(1-\varphi_1(z))p_1(z)}{(1-\varphi_0(z))p_0(z)}\not{\propto}r^*(z)

and so we would get inaccurate estimates of the density ratio no matter how many samples are used to estimate it. The image below demonstrates this in the case were samples in class 1 are more likely to be missing when larger and class 0 has no missingness.

A plot of the density ratio using both the full data and only the observed part of the corrupted data

Our Solution

Our solution to this problem is to use importance weighting. Using relationships between the densities of X and Z we have that

\mathbb{E}[g(Z)]=\mathbb{E}\left[\frac{\mathbb{I}\{X\neq\varnothing\}g(X)}{1-\varphi(X)}\right].

As such we can re-write the KLIEP objective to keep our expectation estimation unbiased even when using these corrupted samples. This gives our modified objective which we call M-KLIEP as follows. Given samples x^0_1,\dotsc,x^0_n from X_0 and samples x^1_1,\dotsc,x^1_n from X_1 our estimate is \hat r=\left(\frac{1}{n}\sum_{i=1}^n\frac{\mathbb{I}\{x_i^0\neq\varnothing\}r(x_i^0)}{1-\varphi_o(x_i^o)}\right)^{-1}\tilde r where \tilde r solves

\underset{r}{\min}~\frac{1}{n}\sum_{i=1}^n\frac{\mathbb{I}\{x_i^1\neq\varnothing\}\log(r(x_i^1))}{1-\varphi_1(x_i^1)}-\log\left(\frac{1}{n}\sum_{i=1}^n\frac{\mathbb{I}\{x_i^0\neq\varnothing\}r(x_i^0)}{1-\varphi_0(x_i^0)}\right).

This objective will now target r^* even when used on MNAR data.

Application to Classification

We now apply our density ratio estimation on MNAR data to estimate the Bayes optimal classifier. Below shows a plot of samples alongside the true Bayes optimal classifier and estimated classifiers from the samples via our method M-KLIEP and a naive method CC-KLIEP which simply ignores missing points. Missing data points are faded out.

Faded points represent missing values. M-KLIEP represents our method, CC-KLIEP represents a Naive approach, BOC gives the Bayes optimal classifier

As we can see, due to not accounting for the MNAR nature of the data, CC-KLIEP underestimates the true number of class 1 samples in the top left region and therefore produces a worse classifier than our approach.

Additional Contributions

As well as this modified objective our paper provides the following additional contributions:

  • Theoretical finite sample bounds on the accuracy of our modified procedure.
  • Methods for learning the missingness functions \varphi_1,\varphi_0.
  • Expansions to partial missingness via a Naive-Bayes framework.
  • Downstream implementation of our method within Neyman-Pearson classification.
  • Adaptations to Neyman-Pearson classification itself making it robust to MNAR data.

For more details see our paper and corresponding github repository. If you have any questions on this work feel free to contact me at josh.givens@bristol.ac.uk.

References

Givens, J., Liu, S., & Reeve, H. W. J. (2023). Density ratio estimation and neyman pearson classification with missing data. In F. Ruiz, J. Dy, & J.-W. van de Meent (Eds.), Proceedings of the 26th international conference on artificial intelligence and statistics (Vol. 206, pp. 8645–8681). PMLR.
Sugiyama, M., Suzuki, T., & Kanamori, T. (2012). Density Ratio Estimation in Machine Learning. Cambridge University Press.

Compass students attending AISTATS 2023 in Valencia

Posted on by josh.givens

We (Ed Davis, Josh Givens, Alex Modell, and Hannah Sansford) attended the 2023 AISTATS conference in Valencia in order to explore the interesting research being presented as well as present some of our own work. While we talked about our work being published at the conference in this earlier blog post, having now attended the conference, we thought we’d talk about our experience there. We’ll spotlight some of the talks and posters which interested us most and talk about our highlights of Valencia as a whole.

Talks & Posters

Mode-Seeking Divergences: Theory and Applications to GANs

One especially interesting talk and poster at the conference was presented by Cheuk Ting Li on their work in collaboration with Farzan Farnia. This work aims to set up a formal classification for various probability measure divergences (such as f-Divergences, Wasserstein distance, etc.) in terms of there mode-seeking or mode-covering properties. By mode-seeking/mode-covering we mean the behaviour of the divergence when used to fit a unimodal distribution to a multi-model target. Specifically a mode-seeking divergence will encourage the target distribution to fit just one of the modes ignoring the other while a mode covering divergence will encourage the distribution to cover all modes leading to less accurate fitting on an individual mode but better covering the full support of the distribution. While these notions of mode-seeking and mode-covering divergences had been discussed before, up to this point there seems to be no formal definition for these properties, and disagreement on the appropriate categorisation of some divergences. This work presents such a definition and uses it to categorise many of the popular divergence methods. Additionally they show how an additive combination a mode seeking f-divergence and the 1-Wasserstein distance retain the mode-seeking property of the f-divergence while being implementable using only samples from our target distribution (rather than knowledge of the distribution itself) making it a desirable divergence for use with GANs.

Talk: https://youtu.be/F7LdHIzZQow

Paper: https://proceedings.mlr.press/v206/ting-li23a.html

Using Sliced Mutual Information to Study Memorization and Generalization in
Deep Neural Networks

The benefit of attending large conferences like AISTATS is having the opportunity to hear talks that are not related to your main research topic. This was the case with a talk by Wongso et. al. was one such talk. Although it did not overlap with any of our main research areas, we all found this talk very interesting.
The talk was on the topic of tracking memorisation and generalisation in deep neural networks (DNNs) through the use of /sliced mutual information/. Mutual information (MI) is commonly used in information theory and represents the reduction of uncertainty about one random variable, given the knowledge of the other. However, MI is hard to estimate in high dimensions, which makes it a prohibitive metric for use in neural networks.
Enter sliced mutual information (SMI). This metric is the average of the MI terms between their one-dimensional projections. The main difference between SMI and MI is that SMI is scalable to high dimensions and scales faster than MI.
Next, let’s talk about memorisation. Memorisation is known to occur in DNNs and is where the DNN fits random labels in training as it has memorised noisy labels in training, leading to bad generalisation. The authors demonstrate this behaviour by fitting a multi-layer perceptron to the MNIST dataset with various amounts of label noise. As the noise increased, the difference between the training and test accuracy became greater.
As the label noise increases, the MI between the features and target variable does not change, meaning that MI did not track the loss in generalisation. However, the authors show that the SMI did track the generalisation. As the label noise increased, the SMI decreased significantly as the MLP’s generalisation got worse. Their main theorem showed that SMI is lower-bounded by a term which includes the spherical soft-margin separation, a quantity which is used to track memorisation and generalisation!
In summary, unlike MI, SMI can track memorization and generalisation in DNNs. If you’d like to know more, you can find the full paper here: https://proceedings.mlr.press/v206/wongso23a.html.

Invited Speakers and the Test of Time Award

As well as the talks on papers that had been selected for oral presentation, each day began with a (longer) invited talk which, for many of us, were highlights of each day. The invited speakers were extremely engaging and covered varied and interesting topics; from Arthur Gretton (UCL) presenting ‘Causal Effect Estimation with Context and Confounders’ to Shakir Mohamed (DeepMind) presenting ‘Elevating our Evaluations: Technical and Sociotechnical Standards of Assessment in Machine Learning’. A favourite amongst us was a talk from Tamara Broderick (MIT) titled ‘An Automatic Finite-Sample Robustness Check: Can Dropping a Little Data Change Conclusions?’. In this talk she addressed a worry that researchers might have when the goal is to analyse a data sample and apply any conclusions to a new population: was a small proportion of the data sample instrumental to the original conclusion? Tamara and collorators propose a method to assess the sensitivity of statistical conclusions to the removal of a very small fraction of the data set. They find that sensitivity is driven by a signal-to-noise ratio in the inference problem, does not disappear asymptotically, and is not decided by misspecification. In experiments they find that many data analyses are robust, but that the conclusions of severeal influential economics papers can be changed by removing (much) less than 1% of the data! A link to the talk can be found here: https://youtu.be/QYtIEqlwLHE

This year, AISTATS featured a Test of Time Award to recognise a paper from 10 years ago that has had a prominent impact in the field. It was awarded to Andreas Damianou and Neil Lawrence for the paper ‘Deep Gaussian Processes’, and their talk was a definite highlight of the conferece. Many of us had seen Neil speak at a seminar at the University of Bristol last year and, being the engaging speaker he is, we were looking forward to hearing him speak again. Rather than focussing on the technical details of the paper, Neils talk concentrated on his (and the machine learning community’s) research philosophy in the years preceeding writing the paper, and how the paper came about – a very interesting insight, and a refreshing break from the many technical talks!

Valencia

There was so much to like about Valencia even from our short stay there. We’ll try and give you a very brief highlight of our favourite things.

Food & Drink:

Obviously Valencia is renowned for being the birthplace of paella and while the paella was good we sampled many other delights our stay. Our collective highlight was the nicest Burrata any of us had ever had which, in a stunning display of individualism, all four of us decided to get on our first day at the conference.

Artist rendition of our 4 meals.

Beach:

About half an hours tram ride from the conference centre are the beaches of Valencia. These stretch for miles as well as having a good 100m in depth with (surprisingly hot) sand covering the lot. We visited these after the end of the conference on the Thursday and despite it being the only cloudy day of the week it was a perfect way to relax at the end of a hectic few days with the pleasantly temperate water being an added bonus.

Architecture:

Valencia has so much interesting architecture scattered around the city centre. One of the most memorable remarkable places was the San Nicolás de Bari and San Pedro Mártir (Church of San Nicolás) which is known as the Sistine chapel of Valencia (according to the audio-guide for the church at least) with its incredible painted ceiling and live organ playing.

Ceiling of the Church of San Nicolás

 

Summer applications deadline for Compass CDT: 12 June 2023

Posted on by crina.radu

We are happy to announce our upcoming applications deadline is 12 June 2023, 23:59 (London UK time zone) for the final few fully funded places to start September 2023. For international applications there are limited scholarship funded places available. Early applications advised.

Compass is offering specific projects for PhD students to study from Sept 2023. We are pleased to announce that there are 4 new project opportunities to study. The full list of the projects/ supervisors has been updated. All the supervisors listed are open to discussion on the projects provided and can also talk to applicants about other project ideas. Please provide a ranked list of 3 projects of interest: 1 = project of highest interest. Project supervisors will be happy to respond to specific questions you have after reading the proposals. Applicants should contact them by email if they wish beforehand.

New PhD Projects available

The full list of the projects/ supervisors.

PhD Project Allocation Process

Application forms will be reviewed based on the 3 ranked projects specified or other proposed topic. Successful applicants will be invited to attend an interview with the Compass admissions tutors and the specific project supervisor. If you are made an offer of PhD study it will be published through the online application system. You will then have 2 weeks to consider the offer before deciding whether to accept or decline.

We welcome applications from all members of our community and are particularly encouraging those from diverse groups, such as members of the LGBT+ and black, Asian and minority ethnic communities, to join us.

APPLICATIONS DEADLINE

12 June 2023, 23:59 (London UK time zone)

APPLY NOW

Advantages of being a Compass Student

  • Stipend – a generous stipend of £22,622 pa tax free, paid in monthly payments. Plus your own expense budget of £1,000 pa towards travel and research activity.
  • No fees – all tuition fees are covered by the EPSRC and University of Bristol.
  • Bespoke training – first year units are designed specifically for the academic needs of each Compass student, which enables students to develop knowledge and capability to pursue cross-disciplinary PhD research.
  • Supervisors – supervisors from across academic disciplines offer a range of research projects.
  • Cohort – Compass students benefit from dedicated offices and collaboration spaces, enabling strong cohort links and opportunities for shared learning and research.

About Compass CDT

A 4-year bespoke PhD training programme in the statistical and computational techniques of data science, with partners from across the University of Bristol, industry and government agencies.

The cross-disciplinary programme offers exciting collaborations across medicine, computer science, geography, economics, life and earth sciences, as well as with our external partners who range from government organisations such as the Office for National Statistics, NCSC and the AWE, to industrial partners such as LV, Improbable, IBM Research, EDF, and AstraZeneca.

Students are co-located with the Institute for Statistical Science in the School of Mathematics, which occupies the Fry Building.

Hear from our students about their experience with the programme

  • Compass has allowed me to advance my statistical knowledge and apply it to a range of exciting applied projects, as well as develop skills that I’m confident will be highly useful for a future career in data science. – Shannon, Cohort 2

  • With the Compass CDT I feel part of a friendly, interactive environment that is preparing me for whatever I move on to next, whether it be in Academia or Industry. – Sam, Cohort 2

  • An incredible opportunity to learn the ever-expanding field of data science, statistics and machine learning amongst amazing people. – Danny, Cohort 1

Compass CDT Video

Find out more about what it means to be a part of the Compass programme from our students in this short video.

APPLICATIONS DEADLINE

12 June 2023, 23:59 (London UK time zone)

APPLY NOW

Student Perspectives: Intro to Recommendation Systems

Posted on by hannah.sansford

A post by Hannah Sansford, PhD student on the Compass programme.

Introduction

Like many others, I interact with recommendation systems on a daily basis; from which toaster to buy on Amazon, to which hotel to book on booking.com, to which song to add to a playlist on Spotify. They are everywhere. But what is really going on behind the scenes?

Recommendation systems broadly fit into two main categories:

1) Content-based filtering. This approach uses the similarity between items to recommend items similar to what the user already likes. For instance, if Ed watches two hair tutorial videos, the system can recommend more hair tutorials to Ed.

2) Collaborative filtering. This approach uses the the similarity between users’ past behaviour to provide recommendations. So, if Ed has watched similar videos to Ben in the past, and Ben likes a cute cat video, then the system can recommend the cute cat video to Ed (even if Ed hasn’t seen any cute cat videos).

Both systems aim to map each item and each user to an embedding vector in a common low-dimensional embedding space E = \mathbb{R}^d. That is, the dimension of the embeddings (d) is much smaller than the number of items or users. The hope is that the position of these embeddings captures some of the latent (hidden) structure of the items/users, and so similar items end up ‘close together’ in the embedding space. What is meant by being ‘close’ may be specified by some similarity measure.

Collaborative filtering

In this blog post we will focus on the collaborative filtering system. We can break it down further depending on the type of data we have:

1) Explicit feedback data: aims to model relationships using explicit data such as user-item (numerical) ratings.

2) Implicit feedback data: analyses relationships using implicit signals such as clicks, page views, purchases, or music streaming play counts. This approach makes the assumption that: if a user listens to a song, for example, they must like it.

The majority of the data on the web comes from implicit feedback data, hence there is a strong demand for recommendation systems that take this form of data as input. Furthermore, this form of data can be collected at a much larger scale and without the need for users to provide any extra input. The rest of this blog post will assume we are working with implicit feedback data.

Problem Setup

Suppose we have a group of n users U = (u_1, \ldots, u_n) and a group of m items I = (i_1, \ldots, i_m). Then we let \mathbf{R} \in \mathbb{R}^{n \times m} be the ratings matrix where position R_{ui} represents whether user u interacts with item i. Note that, in most cases the matrix \mathbf{R} is very sparse, since most users only interact with a small subset of the full item set I. For any items i that user u does not interact with, we set R_{ui} equal to zero. To be clear, a value of zero does not imply the user does not like the item, but that they have not interacted with it. The final goal of the recommendation system is to find the best recommendations for each user of items they have not yet interacted with.

Matrix Factorisation (MF)

A simple model for finding user emdeddings, \mathbf{X} \in \mathbb{R}^{n \times d}, and item embeddings, \mathbf{Y} \in \mathbb{R}^{m \times d}, is Matrix Factorisation. The idea is to find low-rank embeddings such that the product \mathbf{XY}^\top is a good approximation to the ratings matrix \mathbf{R} by minimising some loss function on the known ratings.

A natural loss function to use would be the squared loss, i.e.

L(\mathbf{X}, \mathbf{Y}) = \sum_{u, i} \left(R_{ui} - \langle X_u, Y_i \rangle \right)^2.

This corresponds to minimising the Frobenius distance between \mathbf{R} and its approximation \mathbf{XY}^\top, and can be solved easily using the singular value decomposition \mathbf{R} = \mathbf{U S V}^\top.

Once we have our embeddings \mathbf{X} and \mathbf{Y}, we can look at the row of \mathbf{XY}^\top corresponding to user u and recommend the items corresponding to the highest values (that they haven’t already interacted with).

Logistic MF

Minimising the loss function in the previous section is equivalent to modelling the probability that user u interacts with item i as the inner product \langle X_u, Y_i \rangle, i.e.

R_{ui} \sim \text{Bernoulli}(\langle X_u, Y_i \rangle),

and maximising the likelihood over \mathbf{X} and \mathbf{Y}.

In a research paper from Spotify [3], this relationship is instead modelled according to a logistic function parameterised by the sum of the inner product above and user and item bias terms, \beta_u and \beta_i,

R_{ui} \sim \text{Bernoulli} \left( \frac{\exp(\langle X_u, Y_i \rangle + \beta_u + \beta_i)}{1 + \exp(\langle X_u, Y_i \rangle + \beta_u + \beta_i)} \right).

Relation to my research

A recent influential paper [1] proved an impossibility result for modelling certain properties of networks using a low-dimensional inner product model. In my 2023 AISTATS publication [2] we show that using a kernel, such as the logistic one in the previous section, to model probabilities we can capture these properties with embeddings lying on a low-dimensional manifold embedded in infinite-dimensional space. This has various implications, and could explain part of the success of Spotify’s logistic kernel in producing good recommendations.

References

[1] Seshadhri, C., Sharma, A., Stolman, A., and Goel, A. (2020). The impossibility of low-rank representations for triangle-rich complex networks. Proceedings of the National Academy of Sciences, 117(11):5631–5637.

[2] Sansford, H., Modell, A., Whiteley, N., and Rubin-Delanchy, P. (2023). Implications of sparsity and high triangle density for graph representation learning. Proceedings of The 26th International Conference on Artificial Intelligence and Statistics, PMLR 206:5449-5473.

[3] Johnson, C. C. (2014). Logistic matrix factorization for implicit feedback data. Advances in Neural Information Processing Systems, 27(78):1–9.

 

Compass students attending the Workshop on Functional Inference and Machine Intelligence (FIMI) at ISM Tokyo

Posted on by edward.milsom

A post by Compass CDT students Edward Milsom, Jake Spiteri, Jack Simons, and Sam Stockman.

We (Edward Milsom, Jake Spiteri, Jack Simons, Sam Stockman) attended the 2023 Workshop on Functional Inference and Machine Intelligence (FIMI) taking place on the 14, 15 and 16th of March at the Institute of Statistical Mathematics in Tokyo, Japan. Our attendance to the workshop was to further collaborative ties between the two institutions. The in-person participants included many distinguished academics from around Japan as well as our very own Dr Song Liu. Due to the workshops modest size, there was an intimate atmosphere which nurtured many productive research discussions. Whilst staying in Tokyo, we inevitably sampled some Japanese culture, from Izakayas to cherry blossoms and sumo wrestling!

We thought we’d share some of our thoughts and experiences. We’ll first go through some of our most memorable talks, and then talk about some of our activities outside the workshop.

Talks

Sho Sonoda – Ridgelet Transforms for Neural Networks on Manifolds and Hilbert Spaces

We particularly enjoyed the talk given by Sho Sonoda, a Research Scientist from the Deep Learning Theory group at Riken AIP on “Ridgelet Transforms for Neural Networks on Manifolds and Hilbert Spaces.” Sonoda’s research aims to demystify the black box nature of neural networks, shedding light on how they work and their universal approximation capabilities. His talk provided valuable insights into the integral representations of neural networks, and how they can be represented using ridgelet transforms. Sonoda presented a reconstruction formula from which we see that if a neural network can be represented using ridgelet transforms, then it is a universal approximator. He went on to demonstrate that various types of networks, such as those on finite fields, group convolutional neural networks (GCNNs), and networks on manifolds and Hilbert spaces, can be represented in this manner and are thus universal approximators. Sonoda’s work improves upon existing universality theorems by providing a more unified and direct approach, as opposed to the previous case-by-case methods that relied on manual adjustments of network parameters or indirect conversions of (G)CNNs into other universal approximators, such as invariant polynomials and fully-connected networks. Sonoda’s work is an important step toward a more transparent and comprehensive understanding of neural networks.

Greg Yang – The unreasonable effectiveness of mathematics in large scale deep learning

Greg Yang is a researcher at Microsoft Research who is working on a framework for understanding neural networks called “tensor programs”. Similar to Neural Tangent Kernels and Neural Network Gaussian Processes, the tensor program framework allows us to consider neural networks in the infinite-width limit, where it becomes possible to make statements about the properties of very wide networks. However, tensor programs aim to unify existing work on infinite-width neural networks by allowing one to take the infinite limit of a much wider range of neural network architectures using one single framework.

In his talk, Yang discussed his most recent work in this area, concerning the “maximal update parametrisation”. In short, they show that in this parametrisation, the optimal hyperparameters of very wide neural networks are the same as those for much smaller neural networks. This means that hyperparameter search can be done using small, cheap models, and then applied to very large models like GPT-3, where hyperparameter search would be too expensive. The result is summarised in this figure from their paper “Tensor Programs V: Tuning Large Neural Networks via Zero-Shot Hyperparameter Transfer”, which shows how this is not possible in the standard parametrisation. This work was only possible by building upon the tensor program framework, thereby demonstrating the value of having a solid theoretical understanding of neural networks.

Statistical Seismology Seminar Series

In addition to the workshop, Sam attended the 88th Statistical Seismology seminar in the Risk Analysis Research Centre at ISM https://www.ism.ac.jp/~ogata/Ssg/ssg_statsei_seminarsE.html. The Statistical Seismology Research Group at ISM was created by Emeritus Professor Yosihiko Ogata and is one of the leading global research institutes for statistical seismology. Its most significant output has been the Epidemic-Type Aftershock Sequence (ETAS) model, a point process based earthquake forecasting model that has been the most dominant model for forecasting since its creation by Ogata in 1988.

As part of the Seminar series, Sam gave a talk on his most recent work (Forecasting the 2016-2017 Central Apennines Earthquake Sequence with a Neural Point Process’, https://arxiv.org/abs/2301.09948) to the research group and other visiting academics.

Japan’s interest is earthquake science is due to the fact that they record the most earthquakes in the world. The whole country is in a very active seismic area, and they have the densest seismic network. So even though they might not actually have the most earthquakes in the world (which is most likely Indonesia) they certainly document the most. The evening before flying back to the UK, Sam and Jack felt a magnitude 5.2 earthquake 300km north of Tokyo in the Miyagi prefecture. At that distance all that was felt was a small shudder…

Japan

It’s safe to say that the abundance of delicious food was the most memorable aspect of our trip. In fact, we never had a bad meal! Our taste buds were taken on a culinary journey as we tried a variety of Japanese dishes. From hearty, broth-based bowls of ramen and tsukemen, to fun conveyor-belt sushi restaurants, and satisfying tonkatsu (breaded deep-fried pork cutlet) with sticky rice or spicy udon noodles, we were never at a loss for delicious options. We even had the opportunity to cook our own food at an indoor barbecue!

Aside from the food, we thoroughly enjoyed our time in Tokyo – exploring the array of second-hand clothes shops, relaxing in bath-houses, and trying random things from the abundance of vending machines.

 

Compass students at AISTATS 2023

Posted on by crina.radu

Congratulations to Compass students Josh Givens, Hannah Sansford and Alex Modell who, along with their supervisors have had their papers accepted to be published at AISTATS 2023.

 

‘Implications of sparsity and high triangle density for graph representation learning’

Hannah Sansford, Alexander Modell, Nick Whiteley, Patrick Rubin-Delanchy

Hannah: In this paper we explore the implications of two common characteristics of real-world networks, sparsity and triangle-density, for graph representation learning. An example of where these properties arise in the real-world is in social networks, where, although the number of connections each individual has compared to the size of the network is small (sparsity), often a friend of a friend is also a friend (triangle-density). Our result counters a recent influential paper that shows the impossibility of simultaneously recovering these properties with finite-dimensional representations of the nodes, when the probability of connection is modelled by the inner-product. We, by contrast, show that it is possible to recover these properties using an infinite-dimensional inner-product model, where representations lie on a low-dimensional manifold. One of the implications of this work is that we can ‘zoom-in’ to local neighbourhoods of the network, where a lower-dimensional representation is possible.

The paper has been selected for oral presentation at the conference in Valencia (<2% of submissions). 

 

Density Ratio Estimation and Neyman Pearson Classification with Missing Data

Josh Givens, Song Liu, Henry W J Reeve

Josh: In our paper we adapt the popular density ratio estimation procedure KLIEP to make it robust to missing not at random (MNAR) data and demonstrate its efficacy in Neyman-Pearson (NP) classification. Density ratio estimation (DRE) aims to characterise the difference between two classes of data by estimating the ratio between their probability densities. The density ratio is a fundamental quantity in statistics appearing in many settings such as classification, GANs, and covariate shift making its estimation a valuable goal. To our knowledge there is no prior research into DRE with MNAR data, a missing data paradigm where the likelihood of an observation being missing depends on its underlying value. We propose the estimator M-KLIEP and provide finite sample bounds on its accuracy which we show to be minimax optimal for MNAR data. To demonstrate the utility of this estimator we apply it the the field of NP classification. In NP classification we aim to create a classifier which strictly controls the probability of incorrectly classifying points from one class. This is useful in any setting where misclassification for one class is much worse than the other such as fault detection on a production line where you would want to strictly control the probability of classifying a faulty item as non-faulty. In addition to showing the efficacy of our new estimator in this setting we also provide an adaptation to NP classification which allows it to still control this misclassification probability even when fit using MNAR data.

Student Perspectives: An Introduction to Stochastic Gradient Methods

Posted on by ettore.fincato

A post by Ettore Fincato, PhD student on the Compass programme.

This post provides an introduction to Gradient Methods in Stochastic Optimisation. This class of algorithms is the foundation of my current research work with Prof. Christophe Andrieu and Dr. Mathieu Gerber, and finds applications in a great variety of topics, such as regression estimation, support vector machines, convolutional neural networks.

We can see below a simulation by Emilien Dupont (https://emiliendupont.github.io/) which represents two trajectories of an optimisation process of a time-varying function. This well describes the main idea behind the algorithms we will be looking at, that is, using the (stochastic) gradient of a (random) function to iteratively reach the optimum.

Stochastic Optimisation

Stochastic optimisation was introduced by [1], and its aim is to find a scheme for solving equations of the form \nabla_w g(w)=0 given “noisy” measurements of g [2].

In the simplest deterministic framework, one can fully determine the analytical form of g(w), knows that it is differentiable and admits an unique minimum – hence the problem

w_*=\underset{w}{\text{argmin}}\quad g(w)

is well defined and solved by \nabla_w g(w)=0.

On the other hand, one may not be able to fully determine g(w) because his experiment is corrupted by a random noise. In such cases, it is common to identify this noise with a random variable, say V, consider an unbiased estimator \eta(w,V) s.t. \mathbb{E}_V[\eta(w,V)]=g(w) and to rewrite the problem as

w_*=\underset{w}{\text{argmin}}\quad\mathbb{E}_V[\eta(w,V)].

(more…)

Compass is funded by EPSRC
Skip to toolbar