Cohort 3 research projects confirmed
Our third Cohort of Compass students have confirmed their PhD projects for the next 3 years and are establishing the direction of their own research within the CDT. (more…)
Compass Conference 2022
Our first Compass Conference was held on Tuesday 13th September 2022, hosted in the newly refurbished Fry Building, home to the School of Mathematics. (more…)
Compass student publishes article in Frontiers
Compass student Dan Milner and his academic supervisors have published an article in Frontiers, one of the most cited and largest research publishers in the world. Dan’s work is funded in collaboration with ILRI (International Livestock Research Institute). (more…)
Student Perspectives: An introduction to normalising flows
A post by Dan Ward, PhD student on the Compass programme.
Normalising flows are black-box approximators of continuous probability distributions, that can facilitate both efficient density evaluation and sampling. They function by learning a bijective transformation that maps between a complex target distribution and a simple distribution with matching dimension, such as a standard multivariate Gaussian distribution. (more…)
Access to Data Science Event: start your PhD journey with Compass
Want to find out what a modern PhD in Statistics and Data Science is like?
Student perspectives: Neural Point Processes for Statistical Seismology
A post by Sam Stockman, PhD student on the Compass programme.
Introduction
Throughout my PhD I aim to bridge a gap between advances made in the machine learning community and the age-old problem of earthquake forecasting. In this cross-disciplinary work with Max Werner from the School of Earth Sciences and Dan Lawson from the School of Mathematics, I hope to create more powerful, efficient and robust models for forecasting, that can make earthquake prone areas safer for their inhabitants.
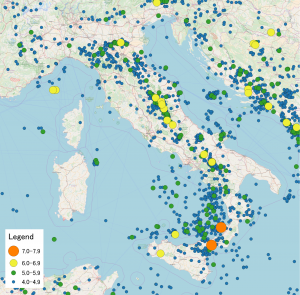
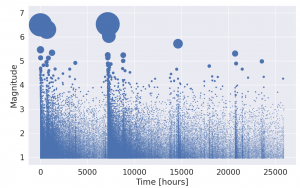
For years seismologists have sought to model the structure and dynamics of the earth in order to make predictions about earthquakes. They have mapped out the structure of fault lines and conducted experiments in the lab where they submit rock to great amounts of force in order to simulate plate tectonics on a small scale. Yet when trying to forecast earthquakes on a short time scale (that’s hours and days, not tens of years), these models based on the knowledge of the underlying physics are regularly outperformed by models that are statistically motivated. In statistical seismology we seek to make predictions through looking at distributions of the times, locations and magnitudes of earthquakes and use them to forecast the future.
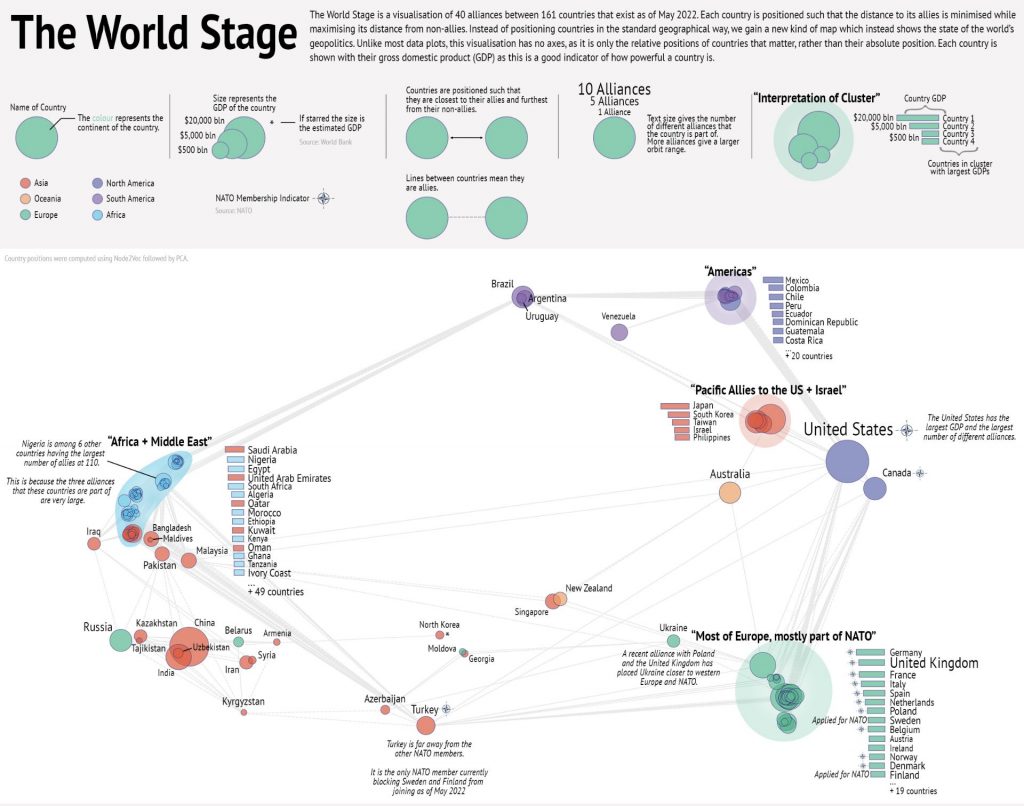
Ed Davis wins poster competition
Congratulations to Ed Davis who won a poster award as part of the Jean Golding Institute’s Beauty of Data competition.
This visualisation, entitled “The World Stage”, gives a new way of representing the positions of countries. Instead of placing them based on their geographical position, they have been placed based on their geopolitical alliances. Countries have been placed such to minimise the distance to their allies and maximise the distance to their non-allies based on 40 different alliances involving 161 countries. This representation was achieved by embedding the alliance network using Node2Vec, followed by principal component analysis (PCA) to reduce it to 2D.
Amazon Web Services: DataScience@Work seminar
Student perspectives: Sampling from Gaussian Processes
A post by Anthony Stephenson, PhD student on the Compass programme.
Introduction
The general focus of my PhD research is in some sense to produce models with the following characteristics:
- Well-calibrated (uncertainty estimates from the predictive process reflect the true variance of the target values)
- Non-linear
- Scalable (i.e. we can run it on large datasets)
At a vague high-level, we can consider that we can have two out of three of those requirements without too much difficulty, but including the third causes trouble. For example, Bayesian linear models would satisfy good-calibration and scalability but (as the name suggests) fail at modelling non-linear functions. Similarly, neural-networks are famously good at modelling non-linear functions and much work has been spent on improving their efficiency and scalability, but producing well-calibrated predictions is a complex additional feature. I am approaching the problem from the angle of Gaussian Processes, which provide well-calibrated non-linear models; at the expense of scalability.
Gaussian Processes (GPs)
See Conor’s blog post for a more detailed introduction to GPs; here I will provide a basic summary of the key facts we need for the rest of the post.
The functional view of GPs is that we define a distribution over functions:
where and
are the mean function and kernel function respectively, which play analogous roles to the usual mean and covariance of a Gaussian distribution.
In practice, we only ever observe some finite collection of points, corrupted by noise, which we can hence view as a draw from some multivariate normal distribution:
where
with
.
(Here subscript denotes dimensionality of the vector or matrix).
When we use GPs to generate predictions at some new test point we use the following equations which I will not derive here (See [1]) for the predicted mean and variance respectively:
The key point here is that both predictive functions involve the inversion of an matrix at a cost of
.

