A post by Tennessee Hickling, PhD student on the Compass programme.
Introduction
Probabilistic modelling provides a consistent way to deal with uncertainty in data. The central tool in this methodology is the probability distribution, which describes the randomness of observations. To create effective models of reality, we need to be able to specify probability distributions that are flexible enough to capture real phenomena whilst remaining feasible to estimate. In the past decade machine learning (ML) has developed many new and exciting ways to represent and learn potentially complex probability distributions.
ML has provided significant advances in modelling of high dimensional and highly structured data such as images or text. Many of these modern approaches are applied as “generative models”. The goal of such approaches is to sample new synthetic observations from an approximate distribution which closely matches the target distribution. For example, we may use many images of cats to learn an approximate distribution, from which we can sample new images of cats that appear realistic. Usually, a “generative model” indicates the requirement to sample from the model, but not necessarily assign probabilities to observed data. In this case, the model captures uncertainty by imitating the structure and randomness of the data.
Many of these modern methods work by transforming simple randomness (such as a Normal distribution) into the target complex randomness. In my own research, I work on a known limitation of such approaches to replicate a particular aspect of randomness – the tails of probability distributions [1, 11]. In this post, I wanted to take a step back and provide an overview of and connections between two ML methods that can be used to model probability distributions – Normalising Flows (NFs) and Variational Autoencoders (VAEs).
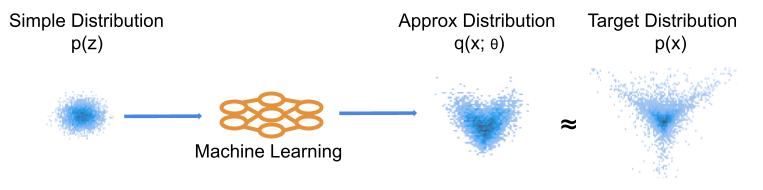
Figure 1: Basic illustration of ML learning of a distribution. We optimise the machine learning model to produce a distribution close to our target. This is often conceptualised in the generative direction, such that our ML model moves samples from the simple distribution to more closely match the target observations.
Some Background
Consider real valued vectors $z \in \mathbb{R}^{d_z}$ and $x \in \mathbb{R}^{d_x}$. In this post I mirror notation used in [2], where $p(x)$ refers to the density and distribution of $x$ and $x \sim p(x)$ indicates samples according to that distribution. The generic set up I am considering is that of density estimation – trying to model the distribution $p(x)$ of some observed data $\{x_i\}_{i=1}^{N}$. I use a semicolon to denote parameters, so $p(x; \beta)$ is a distribution over $x$ with parameters $\beta$. I also make use of different letters to distinguish different distributions, for example using $q(x)$ to denote an approximation to $p(x)$. The notation $\mathbb{E}_p[f(x)]$ refers to the standard expectation of $f(x)$ over the distribution $p$.
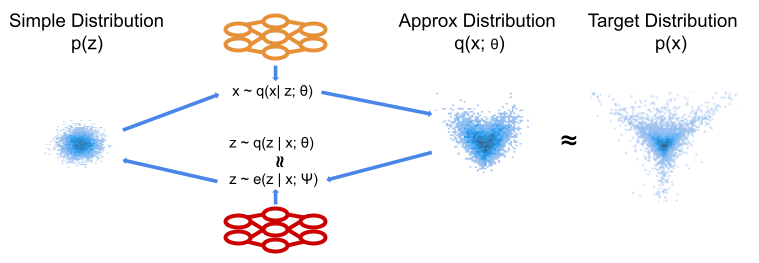
The discussed methods introduce some simple source of randomness arising from a known, simple latent distribution $p(z)$. This is also referred to in some literature as the prior, though the usage is not straightforwardly relatable to traditional Bayesian concepts. The goal is then to fit an approximate $q(x|z; \theta)$, that is a conditional distribution, such that $$q(x; \theta) = \int q(x|z; \theta)p(z)dz \approx p(x),$$in words, the marginal density over $x$ implied by the conditional density, is close to our target distribution $p(x)$. In general, we can’t compute $q(x)$, as we can’t solve the above integral for very flexible $q(x | z; \theta)$.
Variational Inference
We commonly make use of the Kullback-Leibler (KL) divergence, which can be interpreted as measuring the difference between two probability distributions. It is a useful practical tool, since we can compute and optimise the quantity in a wide variety of situations. Techniques which optimise a probability distribution using such divergences are known as variational methods. There are other choices of divergence, but KL is the most standard. Important properties of KL are that the quantity $KL(p|| q)$ is non-negative and non-symmetric i.e. $KL(p|| q) \neq KL(q || p)$.
Given this, we can see that a natural objective is to minimise the difference between distributions, as measured by the KL, $$KL(p(x) || q(x; \theta)) = \int p(x) \log \frac{p(x)}{q(x; \theta)} dx.$$Advances in this area have mostly developed new ways to make this optimisation tractable for flexible $q(x | z; \theta)$.
Normalising Flow
A normalising flow is a parameterised transformation of a random variable. The key simplifying assumption is that the forward generation is deterministic. That is, for $d_x = d_z$, that $$
x = T(z; \theta),$$for some transformation function $T$. We additionally require that $T$ is a differentiable bijection. Given these requirements, we can express the approximate density of $x$ exactly as $$q_x(x; \theta) = p_z(T^{-1}(x; \theta))\big|\text{det } J_{T^{-1}}(x; \theta)\big|.$$Here, $\text{det }J_{T^{-1}}$ is the determinant of the Jacobian of the inverse transformation. Research on NFs has developed numerous ways to make the computation of the Jacobian term tractable. The standard approach is to use neural networks to produce $\theta$ (the parameters of the transformation), with numerous ways of configuring the model to capture dependency between dimensions. Additionally, we often stack many layers to provide more flexibility. See [10] and the review [2] for more details on how this is achieved.
As we have access to an analytic approximate density, we can minimise the negative log-likelihood of our model, $$\mathcal{J}(\theta) = -\sum_{i=1}^{N} \log q(x_i; \theta),$$which is the Monte-Carlo approximation of the KL loss (up to an additive constant). This is straightforward to optimise using stochastic gradient descent [9] and automatic differentiation.
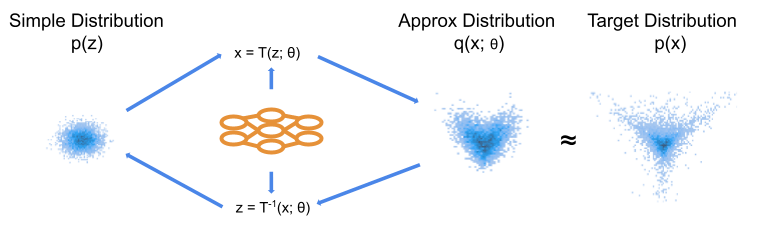
Figure 2: Schematic of NF model. The ML model produces the parameters of our transformation, which are identical in the forward and backwards directions. We choose the transformation such that we can express an analytic density function for our approximate distribution.
Variational Autoencoder
In the Variational Autoencoder (VAE) [3] the conditional distribution $q(x| z; \theta)$ is known as the decoder. VAEs consider the marginal in terms of the posterior, that is $$q(x; \theta) = \frac{q(x | z; \theta)p(z)}{q(z | x; \theta)}.$$The posterior $q(z | x; \theta)$ is itself not generally tractable. VAEs proceed by introducing an encoder, which approximates $q(z | x; \theta)$. This is itself simply a conditional distribution $e(z | x; \psi)$. We use this approximation to express the log marginal over $x$ as below.
$$\begin{align}
\log q(x; \theta) &= \mathbb{E}_{e}\bigg[\log q(x; \theta)\frac{e(z | x; \psi)}{e(z | x; \psi)}\bigg] \\
&= \mathbb{E}_{e}\bigg[\log\frac{q(x | z; \theta)p(z)}{q(z | x; \theta)}\frac{e(z | x; \psi)}{e(z | x; \psi)}\bigg] \\
&= \mathbb{E}_{e}\bigg[\log\frac{q(x | z; \theta)p(z)}{e(z | x; \psi)}\bigg] + KL(e(z | x; \psi) || q(z | x; \theta)) \\
&= \mathcal{J}_{\theta,\psi} + KL(e(z | x; \psi) || q(z | x; \theta))
\end{align}$$
The additional approximation gives a more complex expression and does not provide an analytical approximate density. However, as $KL(e(z | x; \psi) || q(z | x; \theta))$ is positive, $\mathcal{J}_{\theta,\psi}$ forms a lower bound on $\log q(x; \theta)$. This expression is commonly referred to as the Evidence Lower Bound (or ELBO). The second term, the divergence between our encoder and the implied posterior will be minimised as we increase $\mathcal{J}_{\theta,\psi}$ in $\psi$. As we increase $\mathcal{J}_{\theta,\psi}$, we will either be increasing $\log q(x; \theta)$ or reducing $KL(e(z | x; \psi) || q(z | x; \theta))$.
The goal is to increase $\log q(x; \theta)$, which we hope occurs as we optimise over both parameters. This ambiguity in optimisation results in well known issues, such as posterior collapse [12] and can result in some counter-intuitive behaviour [4]. Despite this, VAEs remain a powerful and popular approach. An important benefit is that we no longer require $d_x = d_z$, which means we can map high dimensional $x$ to low dimensional $z$ to perform dimensionality reduction.
Figure 3: Schematic of VAE model. We now have a stochastic forward transformation. To optimise this we introduce a decoder model which approximates the posterior implied by the forward transformation. We now have a more flexible transformation, but two models to train and no analytic approximate density.
Surjective Flows
We can now identify a connection between NFs and VAEs. Recent work has reinterpreted NFs within the VAE framework, permitting a broader class of transitions whilst retaining analytic tractability of NFs [5]. Considering our decoding conditional as $$q(x|z; \theta) = \delta(x – T(z; \theta)),$$ we have the posterior exactly as
$$q(z|x; \theta) = \delta(z – T^{-1}(x; \theta)),$$
where $\delta$ is the dirac delta function.
This provides a view of a NF as a special case of a VAE, where we don’t need to approximate the posterior. Considering our VAE approximation, $$
\log q(x; \theta) = \mathbb{E}_e\big[\log p(z) + \log\frac{q(x | z; \theta)}{e(z | x; \psi)}\big] + KL(e(z | x; \psi) || q(z | x; \theta)),
$$and taking $e(z | x; \psi) = q(z | x; \theta)$, then the final KL term is 0 by definition. In that case, we recover our analytic density for NFs (see [5] for details).
Note that accessing an analytic density depends on having $e(z | x; \psi) = q(z | x; \theta)$ and computing $$\mathbb{E}_e\big[\log p(z) + \log\frac{q(x | z; \theta)}{e(z | x; \psi)}\big].$$These requirements are actually weaker than those we apply in the case of standard NFs. Consider a deterministic transformation $T^{-1}(x)$ which is surjective, crucially we can have many $x$ which map to the same $z$, so no longer have an analytic inverse. However we can still choose a $q(x | z)$ which is stochastic inverse of $T^{-1}$. For example, consider an absolute value surjection, $q(z | x) = \delta(z – |x|)$, to invert this transformation we can choose $q(x | z) = \frac{1}{2}\delta(x – z) + \frac{1}{2}\delta(x + z)$, which we can sample from straight-forwardly. This transformation enforces symmetry across the origin in the approximate distribution, a potentially useful inductive bias. In this example, and many others, we can also compute the density exactly. This has led to a number of interesting extensions to NFs, such as “funnel flows” which have $d_z < d_x$ but retain an analytic approximate density [6]. As we retain an analytic approximate density, we can optimise them in the same way as NFs.
Figure 4: Schematic of a surjective transformation. We have a stochastic forward transformation, but the inverse is deterministic. This restricts what transformations we can have, but retains an analytic approximate density.

Conclusion
I have presented an overview of two widely-used methods for modelling probability distributions with machine learning techniques. I’ve also highlighted an interesting connection between these methods, an area of research that has led to the development of interesting new models. It’s worth noting that other important classes of ML models such as Generative Adversarial Networks and Diffusion models can also be interpreted as approximate probability distributions. There are many superficial connections between those methods and the ones discussed here. Exploring these theoretical similarities presents an compelling direction of research to sharpen understanding of such models’ relative advantages. Another promising direction is the synthesis of these methods, where researchers aim to harness the strengths of each approach [7,8]. This not only enhances the existing knowledge base but also offers opportunities for innovative applications in the field.
References
[1] Jaini, Priyank, et al. “Tails of Lipschitz triangular flows.” International Conference on Machine Learning. PMLR, 2020
[2] Papamakarios, G., et al. “Normalizing flows for probabilistic modeling and inference.” Journal of Machine Learning Research, 2021
[3] Kingma, Diederik P., and Max Welling. “Auto-encoding variational bayes.” arXiv:1312.6114, 2013
[4] Rainforth, Tom, et al. “Tighter variational bounds are not necessarily better.” International Conference on Machine Learning. PMLR, 2018
[5] Nielsen, Didrik, et al. “Survae flows: Surjections to bridge the gap between vaes and flows.” Advances in Neural Information Processing, 2020
[6] Samuel Klein, et al. “Funnels: Exact maximum likelihood with dimensionality reduction.” arXiv:2112.08069, 2021
[7] Kingma, Durk P., et al. “Improved variational inference with inverse autoregressive flow.” Advances in neural information processing systems , 2016
[8] Zhang, Qinsheng, and Yongxin Chen. “Diffusion normalizing flow.” Advances in Neural Information Processing Systems 34, 2021
[9] Ettore Fincato “An Introduction to Stochastic Gradient Methods” https://compass.blogs.bristol.ac.uk/2023/03/14/stochastic-gradient-methods/
[10] Daniel Ward “An introduction to normalising flows” https://compass.blogs.bristol.ac.uk/2022/07/13/2608/
[11] Tennessee Hickling and Dennis Prangle, “Flexible Tails for Normalising Flows, with Application to the Modelling of Financial Return Data”, 8th MIDAS Workshop, ECML PKDD, 2023
[12] Lucas, James, et al. “Don’t blame the elbo! a linear vae perspective on posterior collapse.” Advances in Neural Information Processing Systems 32, 2019

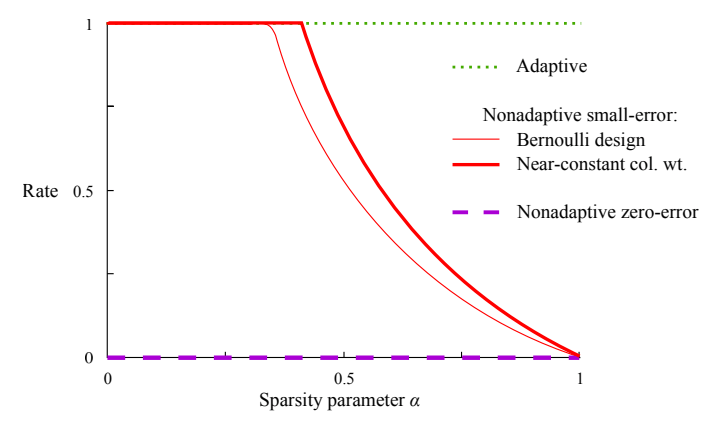 A graph comparing different group testing designs, where the $\text{Rate} = \log_2\binom{n}{k}/T$ where $T$ is the number of tests needed to recover all the defective items (with high probability for the red lines and with certainty for the purple line). [1]
A graph comparing different group testing designs, where the $\text{Rate} = \log_2\binom{n}{k}/T$ where $T$ is the number of tests needed to recover all the defective items (with high probability for the red lines and with certainty for the purple line). [1]